
【题目】已知函数y=f(x)是定义在R上的奇函数,且当x≥0时,f(x)=-x2+ax.
(1)若a=-2,求函数f(x)的解析式;
(2)若函数f(x)为R上的单调减函数,
①求a的取值范围;
②若对任意实数m,f(m-1)+f(m2+t)<0恒成立,求实数t的取值范围.
【答案】(1) ![]() .
.
(2) ①a≤0. ②t> ![]() .
.
【解析】
本试题主要是考查了抽象函数的解析式的求解和单调性的证明以及解不等式。
(1)因为当![]() 时,
时,![]() ,又因为
,又因为![]() 为奇函数,所以
为奇函数,所以![]() ,进而得到解析式。
,进而得到解析式。
(2)根据函数单调性,对于参数a分为正负来讨论得到取值范围。
(3)因为![]() ,∴
,∴![]()
所以![]() 是奇函数,∴
是奇函数,∴![]() ,而又因为
,而又因为![]() 为
为![]() 上的单调递减函数,所以
上的单调递减函数,所以![]() 恒成立,分离参数的思想得到范围。
恒成立,分离参数的思想得到范围。
(1)当![]() 时,
时,![]() ,又因为
,又因为![]() 为奇函数,
为奇函数,
所以![]()
所以![]() …………………………6分
…………………………6分
(2)①当![]() 时,对称轴
时,对称轴![]() ,所以
,所以![]() 在
在![]() 上单调递减,
上单调递减,
由于奇函数关于原点对称的区间上单调性相同,所以![]() 在
在![]() 上单调递减,
上单调递减,
又在![]() 上
上![]() ,在
,在![]() 上
上![]() ,
,
所以当a![]() 0时,
0时,![]() 为R上的单调递减函数
为R上的单调递减函数
当a>0时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,不合题意
上递减,不合题意
所以函数![]() 为单调函数时,a的范围为a
为单调函数时,a的范围为a![]() ………………………………………….10分
………………………………………….10分
②因为![]() ,∴
,∴![]()
所以![]() 是奇函数,∴
是奇函数,∴![]() …………………………12分
…………………………12分
又因为![]() 为
为![]() 上的单调递减函数,所以
上的单调递减函数,所以![]() 恒成立,…………………14分
恒成立,…………………14分
所以![]() 恒成立, 所以
恒成立, 所以![]() …………………………16分
…………………………16分


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两地相距500千米,一辆货车从甲地行驶到乙地,规定速度不得超过100千米![]() 小时.已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
小时.已知货车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度![]() (千米
(千米![]() 时)的平方成正比,比例系数为0.01;固定部分为
时)的平方成正比,比例系数为0.01;固定部分为![]() 元(
元(![]() ).
).
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (千米
(千米![]() 时)的函数,并指出这个函数的定义域;
时)的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知两条公路![]() 的交汇点
的交汇点![]() 处有一学校,现拟在两条公路之间的区域内建一工厂
处有一学校,现拟在两条公路之间的区域内建一工厂![]() ,在两公路旁
,在两公路旁![]() (异于点
(异于点![]() )处设两个销售点,且满足
)处设两个销售点,且满足![]() ,
,![]() (千米),
(千米),![]() (千米),设
(千米),设![]() .
.

(1)试用![]() 表示
表示![]() ,并写出
,并写出![]() 的范围;
的范围;
(2)当![]() 为多大时,工厂产生的噪声对学校的影响最小(即工厂与学校的距离最远).
为多大时,工厂产生的噪声对学校的影响最小(即工厂与学校的距离最远).
(注:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lnx﹣x+a+1
(1)若存在 x∈(0,+∞)使得f(x)≥0成立,求a的范围;
(2)求证:当x>1时,在(1)的条件下, ![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)对任意的实数m,n都有:f(m+n)=f(m)+f(n)-1,
且当x>0时,有f(x)>1.
(1)求f(0).
(2)求证:f(x)在R上为增函数.
(3)若f(1)=2,且关于x的不等式f(ax-2)+f(x-x2)<3对任意的x∈[1,+∞)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:52,54,54,56,56,56,55,55,55,55.若B样本数据恰好是A样本数据都加6后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A. 众数 B. 平均数
C. 中位数 D. 标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国共产党第十九次全国代表大会于2017年10月24日在北京召开,会议提出“决胜全面建成小康社会”.某市积极响应开展“脱贫攻坚”,为2020年“全面建成小康社会”贡献力量.为了解该市农村“脱贫攻坚“情况,从某县调查得到农村居民2011年至2017年家庭人均纯收入![]() (单位:百元)的数据如下表:
(单位:百元)的数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年人均纯收入 | 41 | 45 | 48 | 56 | 60 | 64 | 71 |
注:小康的标准是农村居民家庭年人均纯收入达到8000元.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测2020年该县农村居民家庭年人均纯收入能否达到“全面建成小康社会”的标准?
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
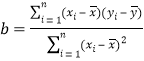 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图.

记![]() 表示
表示![]() 台机器在三年使用期内需更换的易损零件数,
台机器在三年使用期内需更换的易损零件数,![]() 表示
表示![]() 台机器在购买易损零件上所需的费用(单位:元),
台机器在购买易损零件上所需的费用(单位:元),![]() 表示购机的同时购买的易损零件数.
表示购机的同时购买的易损零件数.
(1)若![]() ,求
,求![]() 与
与![]() 的函数解析式;
的函数解析式;
(2)若要求 “需更换的易损零件数不大于![]() ”的频率不小于
”的频率不小于![]() ,求
,求![]() 的最小值;
的最小值;
(3)假设这![]() 台机器在购机的同时每台都购买
台机器在购机的同时每台都购买![]() 个易损零件,或每台都购买
个易损零件,或每台都购买![]() 个易损零件,分别计算这
个易损零件,分别计算这![]() 台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买
台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买![]() 台机器的同时应购买
台机器的同时应购买![]() 个还是
个还是![]() 个易损零件?
个易损零件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com