
设函数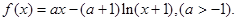
(I)设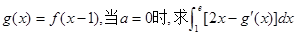 ;
;
(II)求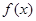 的单调区间;
的单调区间;
(III)当 恒成立,求实数t的取值范围。
恒成立,求实数t的取值范围。
(I)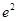 (II)当
(II)当 时,函数
时,函数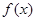 的减区间为
的减区间为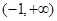 ,无增区间,
,无增区间,
当 时,函数
时,函数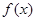 的减区间为
的减区间为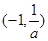 ,增区间为
,增区间为 .(III)
.(III) 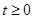 即为所求.
即为所求.
【解析】(I)先求出g(x)的表达式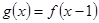
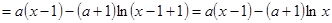 ,
,
然后再利用积分公式求积分即可。
(II)先求出f(x)的导函数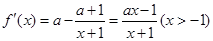 ,
,
然后分a=0,a>0,a<0三种情况进行讨论求其单调区间。
(III)由(II)得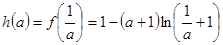 ,
,
因为a>0,所以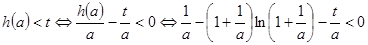 ,
,
然后把 看作整体x,再构造
看作整体x,再构造 ,求其最大值,让m(x)的最大值小于零即可
,求其最大值,让m(x)的最大值小于零即可
(I)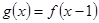

…………1分
当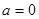 时,
时,
 ,
,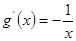 .…………2分
.…………2分
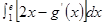
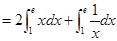


 .…………4分
.…………4分
(II)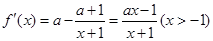 ,…………5分
,…………5分
当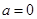 时,
时,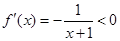 ,
,
所以函数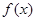 的减区间为
的减区间为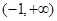 ,无增区间;…………6分
,无增区间;…………6分
当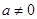 时,
时,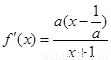 ,
,
若 ,由
,由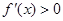 得
得 ,由
,由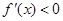 得
得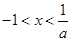 ,
,
所以函数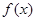 的减区间为
的减区间为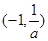 ,增区间为
,增区间为 ;…………7分
;…………7分
若 ,此时
,此时 ,所以
,所以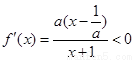 ,
,
所以函数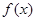 的减区间为
的减区间为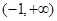 ,无增区间; …………8分
,无增区间; …………8分
综上所述,当 时,函数
时,函数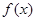 的减区间为
的减区间为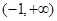 ,无增区间,
,无增区间,
当 时,函数
时,函数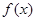 的减区间为
的减区间为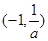 ,增区间为
,增区间为 .…………9分
.…………9分
(III) 由(II)得,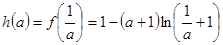 ,…………10分
,…………10分
因为 ,所以
,所以 ,
,
令 ,则
,则 恒成立,
恒成立,
由于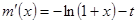 ,
,
① 当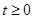 时,
时,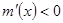 ,故函数
,故函数 在
在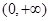 上是减函数,所以
上是减函数,所以
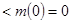 成立;
成立;
② 当 时,若
时,若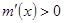 得
得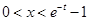 ,故函数
,故函数 在
在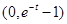 上是增函数,
上是增函数,
即对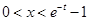 ,
,
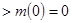 ,与题意不符;
,与题意不符;
综上所述,可以知道,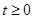 即为所求
即为所求


科目:高中数学 来源:2012届辽宁省辽南协作体高三上学期期中考试理科数学 题型:解答题
(本小题满分12分)
设函数
(I)设 的内角,且为钝角,求
的内角,且为钝角,求 的最小值;
的最小值;
(II)设 是锐角
是锐角 的内角,且
的内角,且 求
求 的三个内角的大小和AC边的
的三个内角的大小和AC边的 长。
长。
查看答案和解析>>
科目:高中数学 来源:2011-2012学年辽宁省辽南协作体高三上学期期中考试理科数学 题型:解答题
(本小题满分12分)
设函数
(I)设 的内角,且为钝角,求
的内角,且为钝角,求 的最小值;
的最小值;
(II)设 是锐角
是锐角 的内角,且
的内角,且 求
求 的三个内角的大小和AC边的长。
的三个内角的大小和AC边的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com