
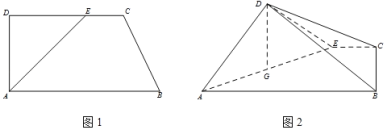
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
, ![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,将
,将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (如图),
(如图),![]() 为
为![]() 中点.
中点.
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求四棱锥![]() 的体积;
的体积;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)见解析(Ⅱ)![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】
(I)证明DG⊥AE,再由面面垂直的性质可得到证明;(II)分别计算DG和梯形ABCE的面积,即可得棱锥体积;(III)过点C作CF∥AE交AB于点F,过点F作FP∥AD交DB于点P,连接PC,可证平面PCF∥平面ADE,故CP∥平面ADE,根据PF∥AD计算![]() 的值.
的值.
(Ⅰ)证明:因为![]() 为
为![]() 中点,
中点,![]() ,
,
所以![]() .
.
因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅱ)在直角三角形![]() 中,易求
中,易求![]() ,则
,则![]() .
.
所以四棱锥![]() 的体积为
的体积为
![]() .
.
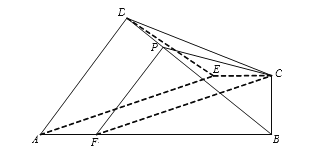
(Ⅲ) 过点C作![]() 交
交![]() 于点
于点![]() ,则
,则![]() .
.
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() .
.
又因为![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
同理![]() 平面
平面![]() .
.
又因为![]() ,
,
所以平面![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以在![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]()


科目:高中数学 来源: 题型:
【题目】如图是某手机商城2018年华为、苹果、三星三种品牌的手机各季度销量的百分比堆积图(如:第三季度华为销量约占![]() ,三星销量约占
,三星销量约占![]() ,苹果销量约占
,苹果销量约占![]() ),根据该图,以下结论中一定正确的是( )
),根据该图,以下结论中一定正确的是( )
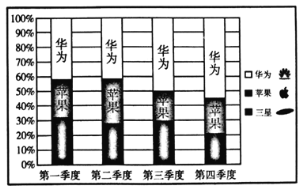
A. 四个季度中,每季度三星和苹果总销量之和均不低于华为的销量
B. 苹果第二季度的销量小于第三季度的销量
C. 第一季度销量最大的为三星,销量最小的为苹果
D. 华为的全年销量最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若曲线![]() 在点
在点![]() 处的切线与x轴平行,求a的值;
处的切线与x轴平行,求a的值;
(Ⅱ)若![]() 在
在![]() 处取得极大值,求a的取值范围;
处取得极大值,求a的取值范围;
(Ⅲ)当a=2时,若函数![]() 有3个零点,求m的取值范围.(只需写出结论)
有3个零点,求m的取值范围.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z满足|z|![]() ,z的实部大于0,z2的虚部为2.
,z的实部大于0,z2的虚部为2.
(1)求复数z;
(2)设复数z,z2,z﹣z2之在复平面上对应的点分别为A,B,C,求(![]() )
)![]()
![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,上顶点为
,上顶点为![]() ,过点
,过点![]() 与
与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于点
轴负半轴于点![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右焦点
的右焦点![]() 作斜率为1的直线
作斜率为1的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,试在
两点,试在![]() 轴上求一点
轴上求一点![]() ,使得以
,使得以![]() ,
,![]() 为邻边的平行四边形是菱形.
为邻边的平行四边形是菱形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() (
(![]() 为常数,
为常数,![]() ,
,![]() ,
,![]() ),给出下列四个结论:①若数列
),给出下列四个结论:①若数列![]() 是周期数列,则周期必为2:②若
是周期数列,则周期必为2:②若![]() ,则数列
,则数列![]() 必是常数列:③若
必是常数列:③若![]() ,则数列
,则数列![]() 是递增数列:④若
是递增数列:④若![]() ,则数列
,则数列![]() 是有穷数列,其中,所有错误结论的序号是________.
是有穷数列,其中,所有错误结论的序号是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com