
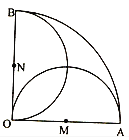
【题目】如图,在圆心角为直角的扇形OAB区域中,M、N分别为OA、OB的中点,在M、N两点处各有一个通信基站,其信号的覆盖范围分别为以OA、OB为直径的圆,在扇形OAB内随机取一点,则此点无信号的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
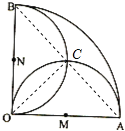
试题OA的中点是M,则∠CMO=90°,这样就可以求出弧OC与弦OC围成的弓形的面积,从而可求出两个圆的弧OC围成的阴影部分的面积,用扇形OAB的面积减去三角形的面积,减去加上两个弧OC围成的面积就是无信号部分的面积,最后根据几何概型的概率公式解之即可.
解:OA的中点是M,则∠CMO=90°,半径为OA=r
S扇形OAB=![]() πr2,S半圆OAC=
πr2,S半圆OAC=![]() π(
π(![]() )2=
)2=![]() πr2,
πr2,
S△OmC=![]() ×
×![]() ×
×![]() =
=![]() r2,
r2,
S弧OC=![]() S半圆OAC﹣S△ODC=
S半圆OAC﹣S△ODC=![]() πr2﹣
πr2﹣![]() r2,
r2,
两个圆的弧OC围成的阴影部分的面积为![]() πr2﹣
πr2﹣![]() r2,
r2,
图中无信号部分的面积为![]() πr2﹣
πr2﹣![]() r2﹣(
r2﹣(![]() πr2﹣
πr2﹣![]() r2)=
r2)=![]() πr2﹣
πr2﹣![]() r2,
r2,
∴无信号部分的概率是:![]() .
.
故选:B.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 为定义域R上的奇函数,且在R上是单调递增函数,函数
为定义域R上的奇函数,且在R上是单调递增函数,函数![]() ,数列
,数列![]() 为等差数列,且公差不为0,若
为等差数列,且公差不为0,若![]() ,则
,则![]() ( )
( )
A. 45B. 15C. 10D. 0
查看答案和解析>>
科目:高中数学 来源: 题型:
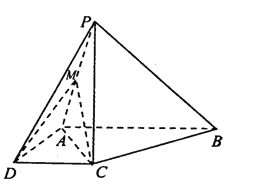
【题目】如图,在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 为线段
为线段![]() 的中点,且过
的中点,且过![]() 三点的平面与线段
三点的平面与线段![]() 交于点
交于点![]() ,确定点
,确定点![]() 的位置,说明理由;并求三棱锥
的位置,说明理由;并求三棱锥![]() 的高.
的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知椭圆C:![]() =1(a>b>0)的左右焦点分别为F1,F2,焦距为2,一条准线方程为x=2.P为椭圆C上一点,直线PF1交椭圆C于另一点Q.
=1(a>b>0)的左右焦点分别为F1,F2,焦距为2,一条准线方程为x=2.P为椭圆C上一点,直线PF1交椭圆C于另一点Q.
(1)求椭圆C的方程;
(2)若点P的坐标为(0,b),求过点P,Q,F2三点的圆的方程;
(3)若![]() =
=![]() ,且λ∈[
,且λ∈[![]() ],求
],求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,过焦点且垂直于x轴的直线被椭圆截得的线段长为3.
,过焦点且垂直于x轴的直线被椭圆截得的线段长为3.
(1)求椭圆的方程;
(2)动直线![]() 与椭圆交于A,B两点,在平面上是否存在定点P,使得当直线PA与直线PB的斜率均存在时,斜率之和是与
与椭圆交于A,B两点,在平面上是否存在定点P,使得当直线PA与直线PB的斜率均存在时,斜率之和是与![]() 无关的常数?若存在,求出所有满足条件的定点P的坐标;若不存在,请说明理由.
无关的常数?若存在,求出所有满足条件的定点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南某地区![]() 年10年间梅雨季节的降雨量
年10年间梅雨季节的降雨量![]() 单位:
单位:![]() 的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
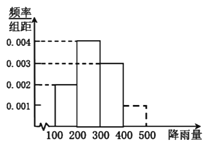
![]() 假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350mm的概率.
假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350mm的概率.
![]() 老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元
老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元![]() 而乙品种杨梅的亩产量
而乙品种杨梅的亩产量![]() 亩
亩![]() 与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为
与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为![]() 元
元![]() ,请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润
,请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润![]() 万元
万元![]() 的期望更大?并说明理由.
的期望更大?并说明理由.
降雨量 |
|
|
|
|
亩产量 | 500 | 700 | 600 | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半圆![]() :
:![]() ,
,![]() 、
、![]() 分别为半圆
分别为半圆![]() 与
与![]() 轴的左、右交点,直线
轴的左、右交点,直线![]() 过点
过点![]() 且与
且与![]() 轴垂直,点
轴垂直,点![]() 在直线
在直线![]() 上,纵坐标为
上,纵坐标为![]() ,若在半圆
,若在半圆![]() 上存在点
上存在点![]() 使
使![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花小镇圈定一块半径为1百米的圆形荒地,准备建成各种不同鲜花景观带.为了便于游客观赏,准备修建三条道路AB,BC,CA,其中A,B,C分别为圆上的三个进出口,且A,B分别在圆心O的正东方向与正北方向上,C在圆心O南偏西某一方向上.在道路AC与BC之间修建一条直线型水渠MN种植水生观赏植物黄鸢尾(其中点M,N分别在BC和CA上,且M在圆心O的正西方向上,N在圆心O的正南方向上),并在区域MNC内种植柳叶马鞭草.
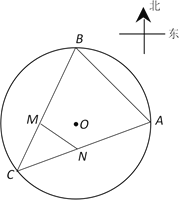
(1)求水渠MN长度的最小值;
(2)求种植柳叶马鞭草区域MNC面积的最大值(水渠宽度忽略不计).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com