练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （16分）如图，w*w^w.k&s#5@u.c~o*m四棱锥S-ABCD的底面是正方形，每条侧棱的长都是地面边长的倍，
    P为侧棱SD上的点。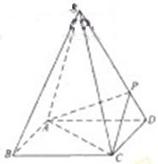
    （Ⅰ）求证：AC⊥SD；       
    （Ⅱ）若SD⊥平面PAC，求二面角P-AC-D的大小
    （Ⅲ）在（Ⅱ）的条件下，侧棱SC上是否存在一点E，使得BE∥平
    面PAC。若存在，求SE：EC的值；若不存在，试说明理由。

    略

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数g（x）=Asin（wx+φ）（A＞0，w＞0，0＜φ＜π）的图象如图所示，其中点A（
    π
    3
    ，2）、B（
    11π
    6
    ，0）分别是函数的最大值点和零点．
    （I）求函数y=g（x）的解析式；
    （Ⅱ）若函数f（x）=2g（x）cosx+m在[0，
    π
    2
    ]上的最大值为6，求函数f（x）在R上的最小值及相应的x值的集合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•乌鲁木齐一模）函数f（x）=2sin（ωx+φ）（ω＞0，0≤φ≤π）的部分图象如图所示，其 中A，B两点之间的距离为5，则f（x）的递增区间是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

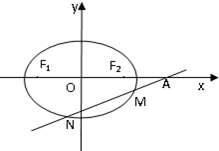    （2012•东城区模拟）已知椭圆C：
    x2
    a2
    +
    y2
    b2
    =1（a＞b＞0）的左、右焦点分别为F1，F2，离心率为
    		2
    2
    ．以原点为圆心，椭圆的短轴长为直径的圆与直线x-y+
    		2
    =0相切．
    （Ⅰ） 求椭圆C的方程；
    （Ⅱ） 如图，若斜率为k（k≠0）的直线l与x轴、椭圆C顺次相交于点A，M，N（A点在椭圆右顶点的右侧），且∠NF2F1=∠MF2A．
    （ⅰ）求证：直线l过定点（2，0）；
    （ⅱ）求斜率k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

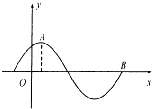    已知函数g（x）=Asin（wx+φ）（A＞0，w＞0，0＜φ＜π）的图象如图所示，其中点A（数学公式，2）、B（数学公式，0）分别是函数的最大值点和零点．
    （I）求函数y=g（x）的解析式；
    （Ⅱ）若函数f（x）=2g（x）cosx+m在[0，数学公式]上的最大值为6，求函数f（x）在R上的最小值及相应的x值的集合．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年湖北省高三（上）期末数学试卷（文科）（解析版） 题型：解答题

    已知函数g（x）=Asin（wx+φ）（A＞0，w＞0，0＜φ＜π）的图象如图所示，其中点A（，2）、B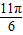（，0）分别是函数的最大值点和零点．
    （I）求函数y=g（x）的解析式；
    （Ⅱ）若函数f（x）=2g（x）cosx+m在[0，]上的最大值为6，求函数f（x）在R上的最小值及相应的x值的集合．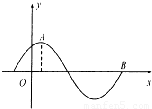

    查看答案和解析>>

    同步练习册答案