Question

设圆C同时满足三个条件：①过原点；②圆心在直线y=x上；③截y轴所得的弦长为4，则圆C的方程是    ．

Answer 1

【答案】分析：分圆心C在第一象限和第三象限两种情况，当圆心C₁在第一象限时，过C₁分别作出与x轴和y轴的垂线，根据角平分线的性质得到四边形OBCD为正方形，连接C₁A，由题意可知圆C与y轴截得的弦长为4，根据垂径定理即可求出正方形的边长即可得到圆心C的坐标，在直角三角形ABC中，利用勾股定理即可求出AC的长即为圆的半径，由圆心和半径写出圆的方程；当圆心C在第三象限时，同理可得圆C的方程．
解答：解：根据题意画出图形，如图所示：

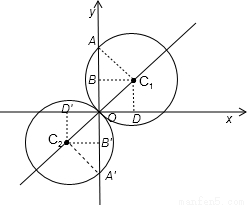
当圆心C₁在第一象限时，过C₁作C₁D垂直于x轴，C₁B垂直于y轴，连接AC₁，
由C₁在直线y=x上，得到C₁B=C₁D，则四边形OBC₁D为正方形，
∵与y轴截取的弦OA=4，∴OB=C₁D=OD=C₁B=2，即圆心C₁（2，2），
在直角三角形ABC₁中，根据勾股定理得：AC₁=2，
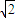
则圆C₁方程为：（x-2）²+（y-2）²=8；
当圆心C₂在第三象限时，过C₂作C₂D垂直于x轴，C₂B垂直于y轴，连接AC₂，
由C₂在直线y=x上，得到C₂B=C₂D，则四边形OB′C₂D′为正方形，
∵与y轴截取的弦OA′=4，∴OB′=C₂D′=OD′=C₂B′=2，即圆心C₂（-2，-2），
在直角三角形A′B′C₂中，根据勾股定理得：A′C₂=2，
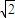
则圆C₁方程为：（x+2）²+（y+2）²=8，
∴圆C的方程为：（x-2）²+（y-2）²=8或（x+2）²+（y+2）²=8．
故答案为：（x-2）²+（y-2）²=8或（x+2）²+（y+2）²=8
点评：此题综合考查了角平分线定理，垂径定理，正方形的性质及直角三角形的性质．学生做题时注意分两种情况，利用数形结合的思想，分别求出圆心坐标和半径，写出所有满足题意的圆的标准方程．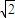