
【题目】已知![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右顶点,
的左、右顶点,![]() 为其右焦点,
为其右焦点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的动点,且
的动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆![]() 的方程及离心率;
的方程及离心率;
(2)直线![]() 与椭圆在点
与椭圆在点![]() 处的切线交于点
处的切线交于点![]() ,当点
,当点![]() 在椭圆上运动时,求证:以
在椭圆上运动时,求证:以![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.
【答案】(1)![]() ,
,![]() ;(2)证明见解析
;(2)证明见解析
【解析】
(1)根据条件和椭圆的性质![]() ,可列方程组,解出
,可列方程组,解出![]() ,即得;(2)设直线
,即得;(2)设直线![]() 的方程为
的方程为![]() ,由直线方程和椭圆方程联立,求出点
,由直线方程和椭圆方程联立,求出点![]() 的坐标,再根据题意求出以
的坐标,再根据题意求出以![]() 为直径的圆,判断该圆是否与直线
为直径的圆,判断该圆是否与直线![]() 恒相切.
恒相切.
(1)由题意可设椭圆![]() 的方程为
的方程为![]() ,
,![]() .
.
由题意知 ,解得
,解得![]() ,
,![]() .
.
故椭圆![]() 的方程为
的方程为![]() ,离心率为
,离心率为![]() .
.
(2)证明:由题意可设直线![]() 的方程为
的方程为![]() .
.
则点![]() 坐标为
坐标为![]() ,
,![]() 中点
中点![]() 的坐标为
的坐标为![]() .
.
由 得
得![]() .
.
设点![]() 的坐标为
的坐标为![]() ,则
,则![]() .
.
所以![]() ,
,![]() .
.
因为点![]() 坐标为
坐标为![]() ,
,
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() .
.
此时以![]() 为直径的圆
为直径的圆![]() 与直线
与直线![]() 相切.
相切.
当![]() 时,则直线
时,则直线![]() 的斜率
的斜率![]() .
.
所以直线![]() 的方程为
的方程为![]() .
.
点![]() 到直线
到直线![]() 的距离
的距离 .
.
又因为![]() ,所以
,所以![]() .
.
故以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切.
相切.
综上得,当点![]() 在椭圆上运动时,以
在椭圆上运动时,以![]() 为直径的圆与直线
为直径的圆与直线![]() 恒相切.
恒相切.


科目:高中数学 来源: 题型:
【题目】如图,设抛物线![]() 与抛物线
与抛物线![]() 在第一象限的交点为
在第一象限的交点为![]() ,点A,B分别在抛物线
,点A,B分别在抛物线![]() ,
,![]() 上,
上,![]() ,
,![]() 分别与
分别与![]() ,
,![]() 相切.
相切.
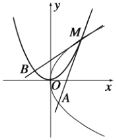
(1)当点M的纵坐标为4时,求抛物线![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),以坐标原点
是参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]()
![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,与曲线
两点,与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 取最大值时
取最大值时![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某有机水果种植基地试验种植的某水果在售卖前要成箱包装,每箱80个,每一箱水果在交付顾客之前要按约定标准对水果作检测,如检测出不合格品,则更换为合格品.检测时,先从这一箱水果中任取10个作检测,再根据检测结果决定是否对余下的所有水果作检测.设每个水果为不合格品的概率都为![]() ,且各个水果是否为不合格品相互独立.
,且各个水果是否为不合格品相互独立.
(Ⅰ)记10个水果中恰有2个不合格品的概率为![]() ,求
,求![]() 取最大值时p的值
取最大值时p的值![]() ;
;
(Ⅱ)现对一箱水果检验了10个,结果恰有2个不合格,以(Ⅰ)中确定的![]() 作为p的值.已知每个水果的检测费用为1.5元,若有不合格水果进入顾客手中,则种植基地要对每个不合格水果支付a元的赔偿费用
作为p的值.已知每个水果的检测费用为1.5元,若有不合格水果进入顾客手中,则种植基地要对每个不合格水果支付a元的赔偿费用![]() .
.
(ⅰ)若不对该箱余下的水果作检验,这一箱水果的检验费用与赔偿费用的和记为X,求EX;
(ⅱ)以检验费用与赔偿费用和的期望值为决策依据,当种植基地要对每个不合格水果支付的赔偿费用至少为多少元时,将促使种植基地对这箱余下的所有水果作检验?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某物流公司专营从甲地到乙地的货运业务(货物全部用统一规格的包装箱包装),现统计了最近100天内每天可配送的货物量,按照可配送货物量T(单位:箱)分成了以下几组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
,并绘制了如图所示的频率分布直方图(同一组数据用该组数据的区间中点值作代表,将频率视为概率).
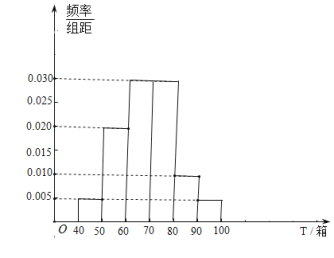
(1)该物流公司负责人决定用分层抽样的方法从前3组中随机抽出11天的数据来分析可配送货物量少的原因,并从这11天的数据中再抽出3天的数据进行财务分析,求这3天的数据中至少有2天的数据来自![]() 这一组的概率.
这一组的概率.
(2)由频率分布直方图可以认为,该物流公司每日的可配送货物量T(单位:箱)服从正态分布![]() ,其中
,其中![]() 近似为样本平均数.
近似为样本平均数.
(ⅰ)试利用该正态分布,估计该物流公司2000天内日货物配送量在区间![]() 内的天数(结果保留整数).
内的天数(结果保留整数).
(ⅱ)该物流公司负责人根据每日的可配送货物量为公司装卸货物的员工制定了两种不同的工作奖励方案.
方案一:直接发放奖金,按每日的可配送货物量划分为以下三级:![]() 时,奖励50元;
时,奖励50元;![]() ,奖励80元;
,奖励80元;![]() 时,奖励120元.
时,奖励120元.
方案二:利用抽奖的方式获得奖金,其中每日的可配送货物量不低于![]() 时有两次抽奖机会,每日的可配送货物量低于
时有两次抽奖机会,每日的可配送货物量低于![]() 时只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为
时只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为
奖金 | 50 | 100 |
概率 |
|
|
小张恰好为该公司装卸货物的一名员工,试从数学期望的角度分析,小张选择哪种奖励方案对他更有利?
附:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为配合“2019双十二”促销活动,某公司的四个商品派送点如图环形分布,并且公司给![]() 四个派送点准备某种商品各50个.根据平台数据中心统计发现,需要将发送给
四个派送点准备某种商品各50个.根据平台数据中心统计发现,需要将发送给![]() 四个派送点的商品数调整为40,45,54,61,但调整只能在相邻派送点进行,每次调动可以调整1件商品.为完成调整,则( )
四个派送点的商品数调整为40,45,54,61,但调整只能在相邻派送点进行,每次调动可以调整1件商品.为完成调整,则( )

A.最少需要16次调动,有2种可行方案
B.最少需要15次调动,有1种可行方案
C.最少需要16次调动,有1种可行方案
D.最少需要15次调动,有2种可行方案
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com