
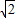 ).
).
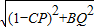 ,可求出MN的长,利用配方法即可求出MN的最小值;
,可求出MN的长,利用配方法即可求出MN的最小值;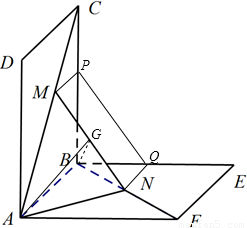 解:(1)作MP∥AB交BC于点,NQ∥AB交BE于点Q,连接PQ,
解:(1)作MP∥AB交BC于点,NQ∥AB交BE于点Q,连接PQ,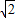 ,CP=BQ=
,CP=BQ=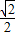 a
a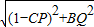 =
=
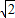 ,
,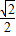 ,即当M、N分别为AC、BF的中点时,MN的长最小,最小为
,即当M、N分别为AC、BF的中点时,MN的长最小,最小为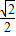 ;
;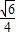 ,所以由余弦定理有cosα=
,所以由余弦定理有cosα=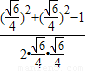 =-
=-
 .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
 如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=
如图,正方形ABCD和四边形ACEF所在的平面互相垂直,CE⊥AC,EF∥AC,AB=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:
8、如图把正方形ABCD沿对角线BD折成直二面角,对于下面结论:查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
如图,正方形ABCD所在平面与等腰三角形EAD所在平面相交于AD,AE⊥平面CDE.
| ||
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com