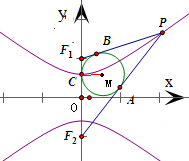
分析:根据题意,设△PF1F2的内切圆分别与PF1、PF2切于点A、B,与F1F2切于点C,由圆的切线长定理得|PA|=|PB|,|F1B|=|F1C|且|F2A|=|F2C|,结合双曲线的定义算出在实轴上的切点C坐标为(0,3).因为CM⊥y轴,所以得到CM所在直线方程为y=3,得到本题答案.
解答:解:∵双曲线的方程为
-=1,
∴a
2=9,b
2=16,得c=
=5
设△PF
1F
2的内切圆分别与PF
1、PF
2切于点A、B,与F
1F
2切于点C,
则|PA|=|PB|,|F
1B|=|F
1C|,|F
2A|=|F
2C|,
又∵点P在双曲线上支上,
∴|PF
2|-|PF
1|=2a=6,
即(|F
2A|+|PA|)-(|F
1B|+|PB|)=6,化简得|F
2A|-|F
1B|=6,
即|F
2C|-|F
1C|=6,而|F
1C|+|F
2C|=2c=10,
设C点坐标为(0,λ),由|F
2C|-|F
1C|=6可得(λ+5)-(5-λ)=6
解之得λ=3,得C的坐标为(0,3)
∵圆M与F
1F
2切于点C,
∴CM⊥y轴,可得CM所在直线方程为y=3
点评:本题给出双曲线的焦点三角形,求三角形的内切圆圆心满足的条件,着重考查了双曲线的定义与简单几何性质、三角形的内切圆、直线与圆的位置关系等知识,属于中档题.




 名校课堂系列答案
名校课堂系列答案