
【题目】已知递增数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,![]() .
.
(1)求证:数列![]() 为等差数列;
为等差数列;
(2)试求所有的正整数![]() ,使得
,使得![]() 为整数;
为整数;
(3)证明: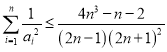 .
.
【答案】(1)见解析(2)![]() (3)见解析
(3)见解析
【解析】
(1)根据![]() ,得出
,得出![]() ,利用
,利用![]() ,即可得出
,即可得出![]() ,
,![]() 或
或![]() ,再结合题意
,再结合题意![]() 为递增数列,确定得
为递增数列,确定得![]() ,结合等差数列定义法,即可证出数列
,结合等差数列定义法,即可证出数列![]() 为等差数列;
为等差数列;
(2)由(1)知,数列![]() 为等差数列,首项为
为等差数列,首项为![]() ,公差
,公差![]() ,则
,则![]() ,化简得
,化简得![]() ,结合
,结合![]() 和
和![]() ,则
,则![]() 且
且![]() 为奇数,即可求出正整数
为奇数,即可求出正整数![]() ;
;
(3)由![]() ,利用放缩法和裂项相消法求和得出
,利用放缩法和裂项相消法求和得出![]() ,进而得出
,进而得出![]() ,要证
,要证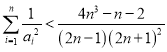 ,则需证
,则需证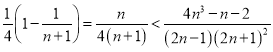 ,转化为证
,转化为证![]() ,
,
当![]() 时,上式显然成立,
时,上式显然成立,![]() 时,原不等式左边为
时,原不等式左边为![]() ,原不等式右边为
,原不等式右边为![]() ,则原不等式成立,从而即可证明
,则原不等式成立,从而即可证明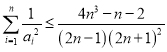 .
.
解:(1)由题可知,![]() ,
,![]() ,
,
则![]() ①,
①,
得![]() ②,
②,
由①-②得:![]() ,
,
即:![]() ,
,
即:![]() ,
,
所以![]() 或
或![]() ,
,
即:![]() 或
或![]() ,
,
若![]() ,则有
,则有![]() ,而
,而![]() ,所以
,所以![]() ,
,
即![]() ,这与数列
,这与数列![]() 递增矛盾,所以
递增矛盾,所以![]() 应舍去,
应舍去,
所以![]() ,故数列
,故数列![]() 为等差数列.
为等差数列.
(2)由(1)知,数列![]() 为等差数列,首项为
为等差数列,首项为![]() ,公差
,公差![]() ,
,
则![]() ,
,
故:![]()
![]()
![]() ,
,
即![]() ,
,
因为![]() ,所以
,所以![]() ,
,
由于![]() ,则
,则![]() 且
且![]() 为奇数,
为奇数,
所以![]() ,故
,故![]() .
.
(3)由(2)可知,![]() ,则
,则![]() ,
,
由于![]() ,
,
即:![]()
所以![]()
即:![]() ,
,
要证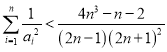 ,则需证
,则需证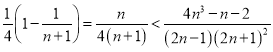 ,
,
即证:![]() ,
,
化为:![]() ,
,
即为:![]() ,
,
当![]() 时,上式显然成立,即
时,上式显然成立,即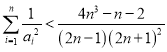 成立,
成立,
又![]() 时,原不等式左边
时,原不等式左边![]() ,原不等式右边
,原不等式右边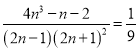 ,则原不等式成立,
,则原不等式成立,
所以综上可得: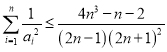 .
.


科目:高中数学 来源: 题型:
【题目】某中学团委组织了“纪念抗日战争胜利73周年”的知识竞赛,从参加竞赛的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() ,…,
,…,![]() 后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:
后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:

(1)求第四组的频率,并补全这个频率分布直方图;
(2)估计这次竞赛的及格率(60分及以上为及格)和平均分(同一组中的数据用该组区间的中点值代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市举行了一次初一学生调研考试,为了解本次考试学生的数学学科成绩情况,从中抽取部分学生的分数(满分为100分,得分取正整数,抽取学生的分数均在![]() 之内)作为样本(样本容量
之内)作为样本(样本容量![]() )进行统计,按照
)进行统计,按照![]() 的分组方法作出频率分布直方图,并作出了样本分数的茎叶图(茎叶图中仅列出了得分在
的分组方法作出频率分布直方图,并作出了样本分数的茎叶图(茎叶图中仅列出了得分在![]() 的数据].
的数据].

(Ⅰ)求频率分布直方图中的![]() 的值,并估计学生分数的中位数;
的值,并估计学生分数的中位数;
(Ⅱ)字在选取的样本中,从成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中恰有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们学校是一所有着悠久传统文化的学校,我们学校全名叫重庆外国语学校(Chongqing Foreign Language School),又名四川外国语大学附属外国语学校,简称“重外”,1981年,被定为四川省首批办好的重点中学;1997年,被列为重庆市教委首批办好的直属重点中学之一;2001年被国家教育部指定为20%高三学生享有保送资格的全国十三所学校之一,今年我校保送取得了非常辉煌的成绩,目前为止,包括清华大学,北京大学在内目前共保送122名同学,其中北京大学,南开大学,北京外国语大学保送的人数成公差为正数的等差数列,三个学校保送人数之和为24人,三个学校保送学生人数之积为312,则北京外国语大学保送的人数为(以上数据均来自于学校官网)( )
A.10B.11C.13D.14
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,
中, ![]() 是坐标原点,设函数
是坐标原点,设函数![]() 的图象为直线
的图象为直线![]() ,且
,且![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,给出下列四个命题:
两点,给出下列四个命题:
①存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有一条;
仅有一条;
②存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有二条;
仅有二条;
③存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有三条;
仅有三条;
④存在正实数![]() ,使
,使![]() 的面积为
的面积为![]() 的直线
的直线![]() 仅有四条.
仅有四条.
其中,所有真命题的序号是( ).
A. ①②③ B. ③④ C. ②④ D. ②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图![]() ,
,![]() 是以
是以![]() 为直径的圆上一段圆弧,
为直径的圆上一段圆弧,![]() 是以
是以![]() 为直径的圆上一段圆弧,
为直径的圆上一段圆弧,![]() 是以
是以![]() 为直径的圆上一段圆弧,三段弧构成曲线
为直径的圆上一段圆弧,三段弧构成曲线![]() .则下面说法正确的是( )
.则下面说法正确的是( )

A.曲线![]() 与
与![]() 轴围成的面积等于
轴围成的面积等于![]()
B.![]() 与
与![]() 的公切线方程为:
的公切线方程为:![]()
C.![]() 所在圆与
所在圆与![]() 所在圆的交点弦方程为:
所在圆的交点弦方程为:![]()
D.用直线![]() 截
截![]() 所在的圆,所得的弦长为
所在的圆,所得的弦长为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下对各事件发生的概率判断正确的是( )
A.甲、乙两人玩剪刀、石头、布的游戏,则玩一局甲不输的概率是![]()
B.从1名男同学和2名女同学中任选2人参加社区服务,则选中一男一女同学的概率为![]()
C.将一个质地均匀的正方体骰子(每个面上分别写有数字1,2,3,4,5,6)先后抛掷2次,观察向上的点数,则点数之和是6的概率是![]()
D.从三件正品、一件次品中随机取出两件,则取出的产品全是正品的概率是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论:
①若![]() ,则“
,则“![]() ”成立的一个充分不必要条件是“
”成立的一个充分不必要条件是“![]() ,且
,且![]() ”;
”;
②存在![]() ,使得
,使得![]() ;
;
③若函数![]() 的导函数是奇函数,则实数
的导函数是奇函数,则实数![]() ;
;
④平面上的动点![]() 到定点
到定点![]() 的距离比
的距离比![]() 到
到![]() 轴的距离大1的点
轴的距离大1的点![]() 的轨迹方程为
的轨迹方程为![]() .
.
其中正确结论的序号为_________.(填写所有正确的结论序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com