
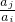 ������������һ������A��
������������һ������A�� ������������{1��3��4}��������{1��3��4} ����������P ��2��
������������{1��3��4}��������{1��3��4} ����������P ��2�� 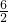 ��
��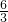 ��
��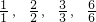 ����������{1��2��3��6}��
����������{1��2��3��6}��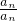 ��������һ������A������ 1��a1��a2����an����anan∉A ��5��
��������һ������A������ 1��a1��a2����an����anan∉A ��5�� 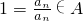 ��6�֡�a1=1 ��7��
��6�֡�a1=1 ��7�� 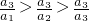 ��a1=1��a2a3∉A����
��a1=1��a2a3∉A����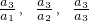 ������A ��8��
������A ��8��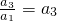 ��
��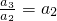 ��
��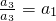 ����a3=a1a3=a22����9��
����a3=a1a3=a22����9��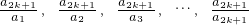 ������A����
������A����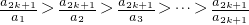 ���Ӷ�����
���Ӷ����� 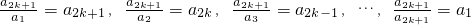 ���� a2k+1=a1a2k+1=a2a2k=a3a2k-1=��=ai+2a2k-i=��=a2ak+2=ak+12 �����~�� ��Ϊai+ja2k-i��ai+2a2k-i=a2k+1��0��i��k-2��3��j��2k-2i�������ԣ�ֻ��
���� a2k+1=a1a2k+1=a2a2k=a3a2k-1=��=ai+2a2k-i=��=a2ak+2=ak+12 �����~�� ��Ϊai+ja2k-i��ai+2a2k-i=a2k+1��0��i��k-2��3��j��2k-2i�������ԣ�ֻ��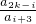 ��
��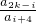 ��
��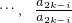 ������A�� ��i ��0 ��k-2 �о٣���õ���
������A�� ��i ��0 ��k-2 �о٣���õ���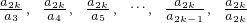 ����2k-2 �
����2k-2 �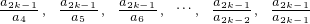 ����2k-4 �
����2k-4 �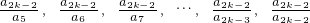 ����2k-6 �
����2k-6 � 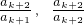 ����2 ���һ��ĵ�2���ܴ�����һ��ĵ�1�
����2 ���һ��ĵ�2���ܴ�����һ��ĵ�1�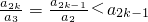 ���ʵ�1��ĸ�������������Ϊ��a2k-2��a2k-3��a2k-4������a2��a1����2��ĸ�������������Ϊ��a2k-4��a2k-5��a2k-6������a2��a1����3��ĸ�������������Ϊ��a2k-6��a2k-7��a2k-8������a2��a1�� ����k-1 ��ĸ�������������Ϊ��a2��a1�����ǣ���
���ʵ�1��ĸ�������������Ϊ��a2k-2��a2k-3��a2k-4������a2��a1����2��ĸ�������������Ϊ��a2k-4��a2k-5��a2k-6������a2��a1����3��ĸ�������������Ϊ��a2k-6��a2k-7��a2k-8������a2��a1�� ����k-1 ��ĸ�������������Ϊ��a2��a1�����ǣ���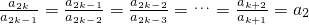 ���ɣ��~����
���ɣ��~����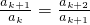 ��
��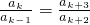 ������
������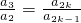 ����
����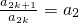 ��������a1��a2������an �ɵȱ����У���15��
��������a1��a2������an �ɵȱ����У���15��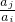 ������������һ������A����֤���ļ��ϼ�{1��3��4}��{1��2��3��6}�е��κ�����Ԫ�صĻ����Ƿ�Ϊ�ü����е�Ԫ�أ�
������������һ������A����֤���ļ��ϼ�{1��3��4}��{1��2��3��6}�е��κ�����Ԫ�صĻ����Ƿ�Ϊ�ü����е�Ԫ�أ�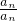 ��������һ������A������ 1��a1��a2����an����anan∉A �Ӷ�
��������һ������A������ 1��a1��a2����an����anan∉A �Ӷ�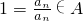 ���a1��ֵ����֤
���a1��ֵ����֤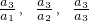 ������A���Ӷ�
������A���Ӷ�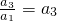 ��
��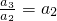 ��
��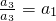 ����a3=a1a3=a22������ȱ����еĶ��壻
����a3=a1a3=a22������ȱ����еĶ��壻


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| aj |
| ai |
| a1+a2+��+an | ||||||
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| aj | ai |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| n | 2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com