
【题目】如图,四棱锥![]() 中,
中,![]() 是正三角形,四边形
是正三角形,四边形![]() 是菱形,点
是菱形,点![]() 是
是![]() 的中点.
的中点.

(I)求证:![]() // 平面
// 平面![]() ;
;
(II)若平面![]() 平面
平面![]() ,
,![]() , 求直线
, 求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)证明见解析;(II)![]() .
.
【解析】
(I)连接BD交AC于点F,再连接EF,利用EF是三角形DBS的中位线,判断出DS平行EF,再利用线面平行的判定得证;
(II)取AB的中点为O,利用已知条件证明DO、SO、BO两两垂直,然后建立空间直角坐标系,求出平面ADC的法向量,再利用线面角的公式求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(I)证明:连接BD角AC于点F,再连接EF.
因为四边形![]() 是菱形,所以点F是BD的中点,
是菱形,所以点F是BD的中点,
又因为点![]() 是
是![]() 的中点,所以EF是三角形DBS的中位线,
的中点,所以EF是三角形DBS的中位线,
所以DS平行EF,
又因为EF![]() 平面ACE,SD
平面ACE,SD![]() 平面ACE
平面ACE
所以![]() // 平面
// 平面![]()
(II)因为四边形![]() 是菱形,
是菱形,![]() ,所以
,所以![]()
又AB=AD,所以三角形ABD为正三角形.
取AB的中点O,连接SO,则DO![]() AB
AB
因为平面![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() =AB
=AB
所以DO![]() 平面ABS,又因为三角形ABS为正三角形
平面ABS,又因为三角形ABS为正三角形
则以O为坐标原点建立坐标系
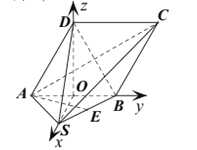
设AB=2a,则![]()
![]()
设平面ADS的一个法向量为![]()
则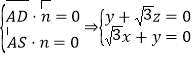
取x=1,则![]()
所以![]()
设直线AC与平面ADS所成角为![]()
则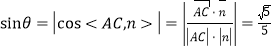


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),在以原点
),在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 有公共点,且直线
有公共点,且直线![]() 与曲线
与曲线![]() 的交点
的交点![]() 恰好在曲线
恰好在曲线![]() 与
与![]() 轴围成的区域(不含边界)内,求
轴围成的区域(不含边界)内,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了更好地服务民众,某共享单车公司通过![]() 向共享单车用户随机派送每张面额为0元,1元,2元的三种骑行券.用户每次使用
向共享单车用户随机派送每张面额为0元,1元,2元的三种骑行券.用户每次使用![]() 扫码用车后,都可获得一张骑行券.用户骑行一次获得1元奖券、获得2元奖券的概率分别是0.5、0.2,且各次获取骑行券的结果相互独立.
扫码用车后,都可获得一张骑行券.用户骑行一次获得1元奖券、获得2元奖券的概率分别是0.5、0.2,且各次获取骑行券的结果相互独立.
(I)求用户骑行一次获得0元奖券的概率;
(II)若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以![]() 为直径的圆上每一点都染上了红、黄、蓝三色之一,已知
为直径的圆上每一点都染上了红、黄、蓝三色之一,已知![]() 、
、![]() 染上了红色,联结圆上的点组成三角形,给出4个结论:
染上了红色,联结圆上的点组成三角形,给出4个结论:
①必定存在一个直角三角形,三个顶点同为红色;
②必定存在一个直角三角形,三个顶点同色;
③必定存在一个直角三角形,三个顶点全不同色;
④必定存在一个直角三角形,或都三个顶点同色,或者三个顶点全不同色。
则真命题的个数是( )个。
A. 1 B. 2
C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知拋物线![]() 的焦点为
的焦点为![]() 是抛物线上横坐标为4且位于
是抛物线上横坐标为4且位于![]() 轴上方的点,点
轴上方的点,点![]() 到抛物线准线的距离等于5.过点
到抛物线准线的距离等于5.过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() 的中点为
的中点为![]() .
.
(1)求抛物线方程;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)以点![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() ,当
,当![]() 是
是![]() 轴上一动点时,讨论直线
轴上一动点时,讨论直线![]() 与圆
与圆![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“五一”期间,为了满足广大人民的消费需求,某共享单车公司欲投放一批共享单车,单车总数不超过100辆,现有A,B两种型号的单车:其中A型车为运动型,成本为400元![]() 辆,骑行半小时需花费
辆,骑行半小时需花费![]() 元;B型车为轻便型,成本为2400元
元;B型车为轻便型,成本为2400元![]() 辆,骑行半小时需花费1元
辆,骑行半小时需花费1元![]() 若公司投入成本资金不能超过8万元,且投入的车辆平均每车每天会被骑行2次,每次不超过半小时
若公司投入成本资金不能超过8万元,且投入的车辆平均每车每天会被骑行2次,每次不超过半小时![]() 不足半小时按半小时计算
不足半小时按半小时计算![]() ,问公司如何投放两种型号的单车才能使每天获得的总收入最多,最多为多少元?
,问公司如何投放两种型号的单车才能使每天获得的总收入最多,最多为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com