
【题目】某理财公司有两种理财产品![]() 和
和![]() .这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
.这两种理财产品一年后盈亏的情况如下(每种理财产品的不同投资结果之间相互独立):
产品![]()
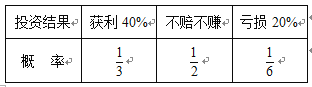
产品![]() (其中
(其中![]() )
)
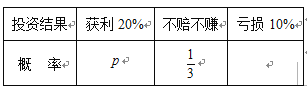
(Ⅰ)已知甲、乙两人分别选择了产品![]() 和产品
和产品![]() 进行投资,如果一年后他们中至少有一人获利的概率大于
进行投资,如果一年后他们中至少有一人获利的概率大于![]() ,求
,求![]() 的取值范围;
的取值范围;
(Ⅱ)丙要将家中闲置的10万元钱进行投资,以一年后投资收益的期望值为决策依据,在产品![]() 和产品
和产品![]() 之中选其一,应选用哪个?
之中选其一,应选用哪个?
【答案】(Ⅰ)![]() .所以
.所以![]() ;(Ⅱ)应选B.
;(Ⅱ)应选B.
【解析】试题分析:
(1)利用题意结合各个事件之间的关系可得![]() .
.
(2)计算数学期望![]() .
.
![]() .
.
则当![]() 时,
时, ![]() ,选择产品
,选择产品![]() 一年后投资收益的数学期望大,应选产品
一年后投资收益的数学期望大,应选产品![]() ;
;
当![]() 时,
时, ![]() ,选择产品
,选择产品![]() 一年后投资收益的数学期望大,应选产品
一年后投资收益的数学期望大,应选产品![]() .
.
试题解析:
(Ⅰ)记事件![]() 为 “甲选择产品
为 “甲选择产品![]() 且盈利”,事件
且盈利”,事件![]() 为“乙选择产品
为“乙选择产品![]() 且盈利”,事件C为“一年后甲、乙两人中至少有一人投资获利”,
且盈利”,事件C为“一年后甲、乙两人中至少有一人投资获利”, ![]() ,
,
所以![]() ,所以
,所以![]() .
.
又因为![]() ,所以
,所以![]() .所以
.所以![]() .
.
(Ⅱ)
假设丙选择产品![]() 进行投资,且记
进行投资,且记![]() 为获利金额(单位:万元),所以随机变量
为获利金额(单位:万元),所以随机变量![]() 的分布列为:
的分布列为:
| 4 | 0 |
|
|
|
|
|
则![]() .
.
假设丙选择产品![]() 进行投资,且记
进行投资,且记![]() 为获利金额(单位:万元),所以随机变量
为获利金额(单位:万元),所以随机变量![]() 的分布列为:
的分布列为:
Y | 2 | 0 |
|
|
|
则![]() .
.
当![]() 时,
时, ![]() ,选择产品
,选择产品![]() 和产品
和产品![]() 一年后投资收益的数学期望相同,可以在产品
一年后投资收益的数学期望相同,可以在产品![]() 和产品
和产品![]() 中任选一个;
中任选一个;
当![]() 时,
时, ![]() ,选择产品
,选择产品![]() 一年后投资收益的数学期望大,应选产品
一年后投资收益的数学期望大,应选产品![]() ;
;
当![]() 时,
时, ![]() ,选择产品
,选择产品![]() 一年后投资收益的数学期望大,应选产品
一年后投资收益的数学期望大,应选产品![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+2x﹣4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(x1 , y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 经过
经过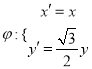 变换后得曲线
变换后得曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)若![]() 为曲线
为曲线![]() 上两点,
上两点, ![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率分别为
的斜率分别为![]() 且
且![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值及此时直线
截得弦长的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=![]() .
.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角A﹣BE﹣P的大小.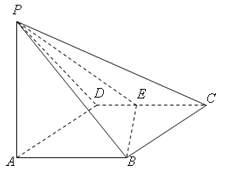
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=![]() (万元).当年产量不小于80千件时,C(x)=51x+
(万元).当年产量不小于80千件时,C(x)=51x+![]() (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(Ⅰ)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() ),曲线
),曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求![]() ,
, ![]() 的值;
的值;
(Ⅱ)证明: ![]() ;
;
(Ⅲ)已知满足![]() 的常数为
的常数为![]() .令函数
.令函数![]() (其中
(其中![]() 是自然对数的底数,
是自然对数的底数, ![]() ),若
),若![]() 是
是![]() 的极值点,且
的极值点,且![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com