

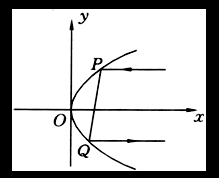
思路解析:由抛物线的光学性质,光源置于抛物镜面的焦点处,光经抛物面反射成一束射出,因此,入射光线与反射光线成平行状态,那么光线PQ必经过抛物线的焦点.
解:由题设知点P的坐标为(a2,a),故直线PQ的方程为:
y=![]() (x-
(x-![]() ),即4ax-(4a2-1)y-a=0.
),即4ax-(4a2-1)y-a=0.
解方程组 得y1=-
得y1=-![]() ,y1=a(舍去),∴x=
,y1=a(舍去),∴x=![]() .
.
∴点Q的坐标为(![]() ,-
,-![]() ).∴|PQ|=|PF|+|FQ|=a2+
).∴|PQ|=|PF|+|FQ|=a2+![]() +
+![]() .
.
要求由入射点P到反射点Q的路程最小时的参数a的值,利用均值不等式,有|PQ|=(a2+![]() )+
)+![]() ≥2
≥2![]() +
+![]() =1.当且仅当a2=
=1.当且仅当a2=![]() ,即a=
,即a=![]() 时,上式等号成立.∴ 入射点P(
时,上式等号成立.∴ 入射点P(![]() ,
,![]() ),反射点Q(
),反射点Q(![]() ,-
,-![]() )时,路程PQ最短,这时P、Q恰关于x轴对称.
)时,路程PQ最短,这时P、Q恰关于x轴对称.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
已知某探照灯的轴截面是抛物线![]() ,如图所示表示平行于对称轴
,如图所示表示平行于对称轴![]() (即
(即![]() 轴)的光线在抛物线上的点
轴)的光线在抛物线上的点![]() 的反射情况,设
的反射情况,设![]() 纵坐标为
纵坐标为![]() ,
,![]() 取何值时,从入射点
取何值时,从入射点![]() 到反射点
到反射点![]() 的光线路程
的光线路程![]() 最短.
最短.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com