
 ,|
,| |=1.则函数y=
|=1.则函数y= 的最大值为 .
的最大值为 .  ,再表示出函数y的表达式整理得到y=282+2(cos
,再表示出函数y的表达式整理得到y=282+2(cos ,sin
,sin )
)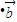 ,最后根据向量模的运算和三角函数的取值范围确定最终答案.
,最后根据向量模的运算和三角函数的取值范围确定最终答案.

 +
+ +2
+2 +…+
+…+ +
+ +2
+2
 )
)
 +cos
+cos +…cos
+…cos ,sin
,sin +sin
+sin +…sin
+…sin )
)
 ,sin
,sin )
)
 ,sin
,sin )
) =|(cos
=|(cos ,sin
,sin )||
)|| |cosθ(θ为向量(cos
|cosθ(θ为向量(cos ,sin
,sin )与向量
)与向量 的夹角)
的夹角) ,sin
,sin )||
)|| |=1
|=1

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com