Question

【题目】已知椭圆，离心率为，两焦点分别为，过的直线交椭圆于两点，且的周长为8.

（1）求椭圆的方程；

（2）过点作圆的切线交椭圆于两点，求弦长的最大值．

Answer 1

【答案】（1）（2）

【解析】试题分析：（1）求椭圆标准方程，一般利用待定系数法，即根据条件列两个独立方程：一是离心率，二是椭圆定义： 的周长为，解方程组得， （2）涉及弦长问题，一般利用直线方程与椭圆方程联立方程组，结合韦达定理和弦长公式求弦长：设切线的方程为，则，再根据直线与圆相切得，即，代入化简得，最后利用基本不等式求最值

试题解析：（1）由题得： ，．．．．．．．．．．．．．．．．．．．．．．．．1分

，．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分

所以．．．．．．．．．．．．．．．．．．．．．．．．．4分

又，所以，．．．．．．．．．．．．．．．．．．．．．．．．5分

即椭圆的方程为．．．．．．．．．．．．．．．．．．．．6分

（2）由题意知， ，设切线的方程为，

由，得．．．．．．．．．．．．．．．7分

设，

则．．．．．．．．．．．．．．．．．．．．．8分

，

由过点的直线与圆相切得，即，

所以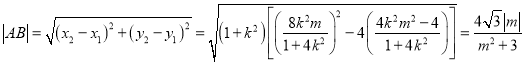．．．．11分

，

当且仅当时， ，所以的最大值为2．．．．．．．．．．．．．．．．．．．12分