


科目:高中数学 来源: 题型:
| a |
| b |
| 3 |
| a |
| b |
| π |
| 2 |
| 1 |
| 6 |
| π |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:044
关于x的方程x2+x·sin2θ-sinθcotθ=0的两根为α,β,且0<θ<2π,若数列1,(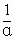 +
+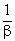 ),
),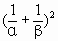 ,…的前100项和为0,
,…的前100项和为0,
(文)求sinθ的值.
(理)求θ的值.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| a |
| b |
| 3 |
| a |
| b |
| π |
| 2 |
| 1 |
| 6 |
| π |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012年江西省上饶市高考数学一模试卷(理科)(解析版) 题型:填空题
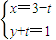 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,则曲线C1与曲线C2有 个公共点.
,以极点为原点,极轴为x轴正半轴建立直角坐标系,则曲线C1与曲线C2有 个公共点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com