
(本题13分)
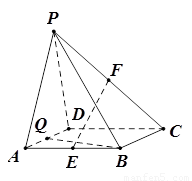
如图,在四棱锥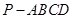 中,
中,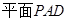
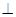 平面
平面 ,底面
,底面 是菱形,
是菱形,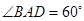 .
.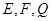 分别是
分别是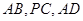 的中点.
的中点.
(1) 求证: ;
;
(2) 求证: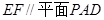 .
.
(1)先证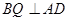 ,根据面面垂直的性质定理可知
,根据面面垂直的性质定理可知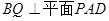
(2)先证FG//AE,且FG=AE,再证AG//EF,根据线面平行的判定定理可证.
【解析】
试题分析:(1)在菱形ABCD中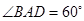 ,所以,AB=BD,
,所以,AB=BD,
因为Q是AD的中点,
所以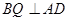 ,且
,且 ,
,
又因为,平面PAD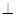 平面ABCD,平面PAD
平面ABCD,平面PAD 平面ABCD=AD,
平面ABCD=AD,
所以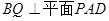 . ……6分
. ……6分
(2)取PD中点G,连接AG,FG,
因为E、F分别是AB,PC中点,
所以FG//AE,且FG=AE,
所以,四边形AEFG为平行四边形,所以,AG//EF
又因为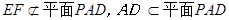
所以 。 ……13分
。 ……13分
考点:本小题主要考查线面垂直和线面平行的证明,考查学生的空间想象能力和推理能力.
点评:要证明线面垂直和线面平行,要紧扣相应的定理的条件,定理中的条件要一一列出来,缺一不可.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源:2011-2012学年广东省高三下学期第一次月考理科数学试卷(解析版) 题型:解答题
(本题满分13分)
如图一,平面四边形 关于直线
关于直线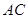 对称,
对称,
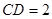 。
。
把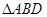 沿
沿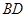 折起(如图二),使二面角
折起(如图二),使二面角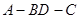 的余弦值等于
的余弦值等于 。对于图二,
。对于图二,

(Ⅰ)求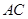 ;
;
(Ⅱ)证明: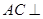 平面
平面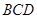 ;
;
(Ⅲ)求直线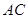 与平面
与平面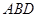 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源:2014届北京师大附中高一第二学期期中考试数学试卷(解析版) 题型:解答题
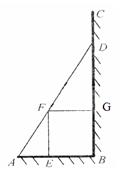
(本题13分)如图,某小区准备在一直角围墙ABC内的空地上植造一块“绿地△ABD”,其中AB长为定值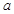 ,BD可长根据需要进行调节(BC足够长)。现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积
,BD可长根据需要进行调节(BC足够长)。现规划在△ABD的内接正方形BEFG内种花,其余地方种草,且把种草的面积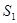 与种花的面积
与种花的面积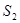 的比值
的比值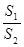 称为“草花比y”。
称为“草花比y”。
(1)设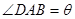 ,将
,将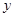 表示成
表示成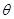 的函数关系式;
的函数关系式;
(2)当BE为多长时,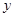 有最小值?最小值是多少?
有最小值?最小值是多少?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆八中高三第六次月考数学文卷 题型:解答题
((本题满分13分)
如图,长方体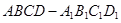 中,
中,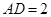 ,
,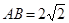 ,
,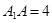 ,
,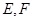 分别是
分别是 的中点.
的中点.

(1)求证: ⊥平面
⊥平面 ;
;
(2)求二面角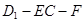 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题13分)如图,四棱锥![]() 的底面是边长为
的底面是边长为![]() 的菱形,
的菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() 为
为![]() 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;
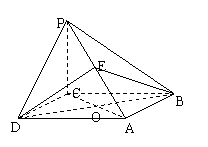 (1)求BE 与 CD所成的角.;
(1)求BE 与 CD所成的角.;
(2)求二面角![]() 的正切值。
的正切值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com