

| 解:(1)如图,取AC的中点E,连结DE、PE,则DE∥BC, 所以∠PDE(或其补角)为异面直线PD与BC所成的角, 因为BC∥DE,AC⊥BC,所以AC⊥DE; 又PC⊥平面ABC,DE 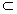 平面ABC,所以PC⊥DE, 平面ABC,所以PC⊥DE,因为AC∩PC=C,所以DE⊥平面PAC, 因为PE 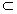 平面PAC,所以DE⊥PE, 平面PAC,所以DE⊥PE,在Rt△ABC中,因为AC=BC=2,所以AB=2  , ,在Rt△PCD中,因为PC=2,CD= 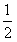 AB= AB=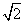 ,所以PD= ,所以PD=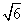 , ,在Rt△PDE中,因为DE= 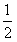 BC=1,所以cos∠PDE= BC=1,所以cos∠PDE=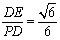 , ,即异面直线PD与BC所成的角为arccos 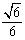 。 。(2)因为BC⊥AC,BC⊥PC,AC∩PC =C,所以BC⊥平面PAC,即BC⊥平面PCM, 又BC 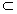 平面BCM, 平面BCM,所以平面PCM⊥平面BCM, 过点A作AN⊥CM交CM于N,则AN⊥平面BCM, 在Rt△PAC中,AC=PC=2,所以AP=2 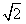 , ,又AP=4AM,所以AM= 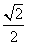 , ,△ACM中,∠MAC=45°, 所以CM= 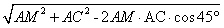 = =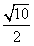 , ,过M作MG⊥AC交AC于G,MG=AMsin45°= 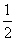 , ,由  MG·AC= MG·AC=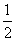 AN·CM,得AN= AN·CM,得AN=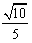 , ,所以,点A到平面BCM的距离为 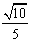 。 。 |
 |


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
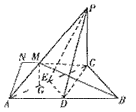
如图,PC⊥平面ABC,∠ACB=90°,D为AB中点,
AC=BC=PC=2.
(Ⅰ)求证:AB⊥平面PCD;
(Ⅱ)求异面直线PD与BC所成角的大小;
(Ⅲ)设M为线段PA上的点,且AP=4AM,求点A到平面BCM的距离.
查看答案和解析>>
科目:高中数学 来源:河北省2009-2010学年高二第四次考试(数学)试题 题型:解答题
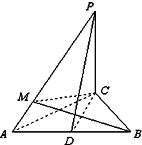
如图,PC⊥平面ABC,∠ACB=90°,D为AB中点,
AC=BC=PC=2.
(Ⅰ)求证:AB⊥平面PCD;
(Ⅱ)求异面直线PD与BC所成角的大小;
(Ⅲ)设M为线段PA上的点,且AP=4AM,求点A到平面BCM的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
如图,PC⊥平面ABC,∠ACB=90°,D为AB中点, AC=BC=PC=2.
(Ⅰ)求证:AB⊥平面PCD;
(Ⅱ)求异面直线PD与BC所成角的大小;
(Ⅲ)设M为线段PA上的点,且AP=4AM,求点A到平面BCM的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
如图,PC⊥平面ABC,∠ACB=90°,D为AB中点,AC=BC=PC=2.
(I)求证:AB⊥平面PCD;
(II)求异面直线PD与BC所成的角的余弦值;
(III)求点C到平面PAD的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com