
【题目】如图,在四棱锥![]() 中,四边形ABCD为平行四边形,且
中,四边形ABCD为平行四边形,且![]() ,
,![]() ,
,![]() 平面PAC.
平面PAC.

(1)求证:![]() 平面
平面![]() ;
;
(2)若异面直线PC与AD所成的角为30°,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据线面垂直判断定理:如果一条直线垂直一个平面内的两条相交线,那么这条线垂直这个平面,要证![]() 平面
平面![]() ,只需证明
,只需证明![]() 和
和![]() ,即可求得答案;
,即可求得答案;
(2)先求证![]() 平面
平面![]() ,以A为坐标原点,AB,AC所在直线分别为x,y轴,过点A且与PE平行的直线为z轴,建立空间直角坐标系,求得平面PBC的法向量为
,以A为坐标原点,AB,AC所在直线分别为x,y轴,过点A且与PE平行的直线为z轴,建立空间直角坐标系,求得平面PBC的法向量为![]() ,平面PDC的法向量为
,平面PDC的法向量为![]() ,根据
,根据 ,即可求得答案.
,即可求得答案.
(1)在![]() 中,
中,![]() ,
,![]() ,
,
由余弦定理得:
![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,![]() ,即
,即![]()
![]()
![]() 平面PAC,
平面PAC,![]() 平面PAC,
平面PAC,
![]()
![]() .
.
又![]()
![]() 平面PAB,
平面PAB,![]() 平面PAB,
平面PAB,![]() ,
,
![]()
![]() 平面PAB.
平面PAB.
(2)![]()
![]() ,
,
![]()
![]() 是异面直线PC与AD所成的角,
是异面直线PC与AD所成的角,
又![]()
![]() 平面
平面![]() ,
,
![]()
![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,易知
,易知![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]()
![]() ,取AB的中点E,连接PE,则
,取AB的中点E,连接PE,则![]() .
.
由(1)知![]() 平面PAB,
平面PAB,
![]()
![]() ,
,
又![]()
![]() 平面
平面![]() ,
,![]() 平面ABCD,
平面ABCD,![]() ,
,
![]()
![]() 平面ABCD,
平面ABCD,
如图,以A为坐标原点,AB,AC所在直线分别为x,y轴,过点A且与PE平行的直线为z轴,建立空间直角坐标系,

则![]() ,
,![]() ,
,![]() ,
, ,
,
可得: ,
,![]() ,
,![]() ,
,
设平面PBC的法向量为![]() ,
,
则
取![]() ,则
,则![]() ,
,
![]()
![]() ,是平面PBC的一个法向量
,是平面PBC的一个法向量
设平面PDC的法向量为![]() ,
,
则 ,
,
则![]() ,取
,取![]() ,则
,则![]() ,
,
![]()
![]() ,是平面PDC的一个法向量.
,是平面PDC的一个法向量.
![]()
 ,
,
由图可知二面角![]() 是钝二面角,
是钝二面角,
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2017年种植的一批试验紫甘薯在温度升高时6组死亡的株数:

经计算: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,其中
,其中![]() 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数, ![]() .
.
(1)若用线性回归模型,求![]() 关于
关于![]() 的回归方程
的回归方程![]() (结果精确到
(结果精确到![]() );
);
(2)若用非线性回归模型求得![]() 关于
关于![]() 的回归方程为
的回归方程为![]() ,且相关指数为
,且相关指数为![]() .
.
(i)试与(1)中的回归模型相比,用![]() 说明哪种模型的拟合效果更好;
说明哪种模型的拟合效果更好;
(ii)用拟合效果好的模型预测温度为![]() 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).
附:对于一组数据![]() ,
, ![]() ,……,
,……, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:  ;相关指数为:
;相关指数为:  .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() .已知
.已知![]() 分别是
分别是![]() 的中点.将
的中点.将![]() 沿
沿![]() 折起,使
折起,使![]() 到
到![]() 的位置且二面角
的位置且二面角![]() 的大小是60°,连接
的大小是60°,连接![]() ,如图:
,如图:
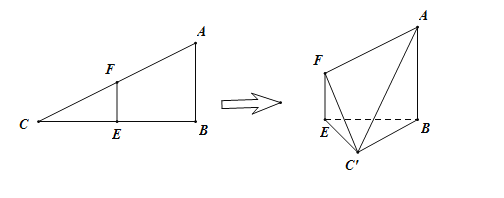
(1)证明:平面![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成二面角的大小.
所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于某种类型的口服药,口服![]() 小时后,由消化系统进入血液中药物浓度
小时后,由消化系统进入血液中药物浓度![]() (单位)与时间
(单位)与时间![]() 小时的关系为
小时的关系为![]() ,其中
,其中![]() ,
,![]() 为常数,对于某一种药物
为常数,对于某一种药物![]() ,
,![]() ,
,![]() .
.
(1)口服药物后______小时血液中药物浓度最高;
(2)这种药物服药![]() 小时后血液中药物浓度如下表
小时后血液中药物浓度如下表
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 0.9545 | 0.9304 | 0.6932 | 0.4680 | 0.3010 | 0.1892 | 0.1163 | 0.072 |
一个病人上午8:00第一次服药,要使得病人血液中药物浓度保持在0.5个单位以上,第三次服药时间是______(时间以整点为准)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从甲乙两个教师所教班级的学生中随机抽取100人,每人分别对两个教师进行评分,满分均为100分,整理评分数据,将分数以10为组距分成6组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .得到甲教师的频率分布直方图,和乙教师的频数分布表:
.得到甲教师的频率分布直方图,和乙教师的频数分布表:
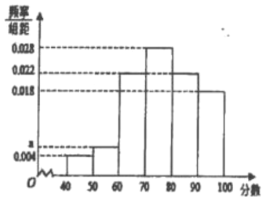
乙教师分数频数分布表 | |
分数区间 | 频数 |
| 3 |
| 3 |
| 15 |
| 19 |
| 35 |
| 25 |
(1)在抽样的100人中,求对甲教师的评分低于70分的人数;
(2)从对乙教师的评分在![]() 范围内的人中随机选出2人,求2人评分均在
范围内的人中随机选出2人,求2人评分均在![]() 范围内的概率;
范围内的概率;
(3)如果该校以学生对老师评分的平均数是否大于80分作为衡量一个教师是否可评为该年度该校优秀教师的标准,则甲、乙两个教师中哪一个可评为年度该校优秀教师?(精确到0.1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是EA的中点(如图1),将
是EA的中点(如图1),将![]() 沿CD折起到图2中
沿CD折起到图2中![]() 的位置,得到四棱锥是
的位置,得到四棱锥是![]() .
.
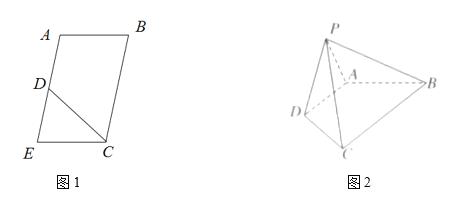
(1)求证:![]() 平面PDA;
平面PDA;
(2)若PD与平面ABCD所成的角为![]() .且
.且![]() 为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
为锐角三角形,求平面PAD和平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
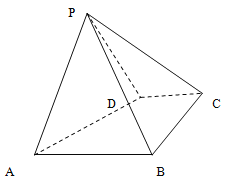
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,且
,且![]() 是以
是以![]() 为底的等腰三角形.
为底的等腰三角形.
(Ⅰ)证明:![]()
(Ⅱ)若四棱锥![]() 的体积等于
的体积等于![]() .问:是否存在过点
.问:是否存在过点![]() 的平面
的平面![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由团中央学校部、全国学联秘书处、中国青年报社共同举办的2018年度全国“最美中学生”寻访活动结果出炉啦,此项活动于2018年6月启动,面向全国中学在校学生,通过投票方式寻访一批在热爱祖国、勤奋学习、热心助人、见义勇为等方面表现突出、自觉树立和践行社会主义核心价值观的“最美中学生”.现随机抽取了30名学生的票数,绘成如图所示的茎叶图,若规定票数在65票以上(包括65票)定义为风华组.票数在65票以下(不包括65票)的学生定义为青春组.
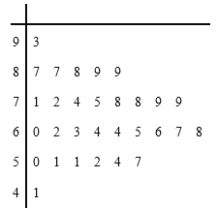
(1)如果用分层抽样的方法从青春组和风华组中抽取5人,再从这5人中随机抽取2人,那么至少有1人在青春组的概率是多少?
(2)用样本估计总体,把频率作为概率,若从该地区所有的中学(人数很多)中随机选取4人,用![]() 表示所选4人中青春组的人数,试写出
表示所选4人中青春组的人数,试写出![]() 的分布列,并求出
的分布列,并求出![]() 的数学期望.
的数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com