
(13分)已知函数 .
.
(1)讨论函数 的单调性;
的单调性;
(2)若曲线 上两点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.
上两点A、B处的切线都与y轴垂直,且线段AB与x轴有公共点,求实数a的取值范围.
(1)若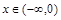 ,则
,则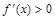 ,所以
,所以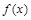 在区间
在区间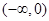 上是增函数;
上是增函数;
若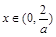 ,则
,则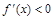 ,所以
,所以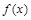 在区间
在区间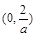 上是减函数;
上是减函数;
若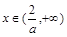 ,则
,则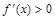 ,所以
,所以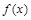 在区间
在区间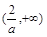 上是增函数;
上是增函数;
(2)实数a的取值范围是[-1,0)∪[3,4].
【解析】解:由题设知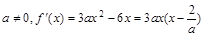 .
.
令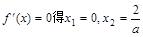 .
.
当(i)a>0时,
若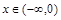 ,则
,则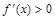 ,所以
,所以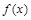 在区间
在区间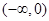 上是增函数;
上是增函数;
若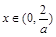 ,则
,则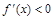 ,所以
,所以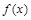 在区间
在区间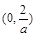 上是减函数;
上是减函数;
若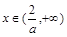 ,则
,则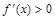 ,所以
,所以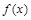 在区间
在区间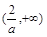 上是增函数;
上是增函数;
(i i)当a<0时,
若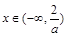 ,则
,则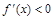 ,所以
,所以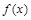 在区间
在区间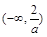 上是减函数;
上是减函数;
若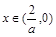 ,则
,则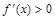 ,所以
,所以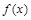 在区间
在区间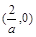 上是增函数;
上是增函数;
若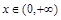 ,则
,则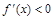 ,所以
,所以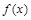 在区间
在区间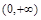 上是减函数.
上是减函数.
(2)由(Ⅰ)的讨论及题设知,曲线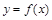 上的两点A、B的纵坐标为函数的极值,且函数
上的两点A、B的纵坐标为函数的极值,且函数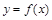 在
在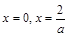 处分别是取得极值
处分别是取得极值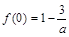 ,
, .
.
因为线段AB与x轴有公共点,所以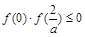 .
.
即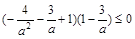 .所以
.所以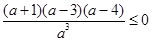 .
.
故a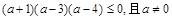 .
.
解得 -1≤a<0或3≤a≤4.
即所求实数a的取值范围是[-1,0)∪[3,4].


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com