
设函数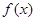 是定义在
是定义在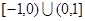 上的偶函数,当
上的偶函数,当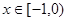 时,
时,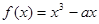 (
(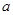 是实数)。
是实数)。
(1)当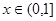 时,求f(x)的解析式;
时,求f(x)的解析式;
(2)若函数f(x)在(0,1]上是增函数,求实数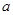 的取值范围;
的取值范围;
(3)是否存在实数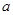 ,使得当
,使得当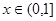 时,f(x)有最大值1.
时,f(x)有最大值1.
(1)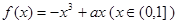
(2)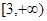
(3)存在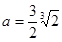 使得当
使得当 时,f(x)有最大值1
时,f(x)有最大值1
【解析】本试题主要是考查了函数的奇偶性和单调性以及函数的最值的综合运用。
(1)因为函数 是定义在
是定义在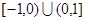 上的偶函数,当
上的偶函数,当 时的解析式,利用偶函数的的对称性得到结论。
时的解析式,利用偶函数的的对称性得到结论。
(2)因为给定区间单调递增,即当 时,
时,
所以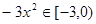 因为f(x)在(0,1]上是增函数,所以
因为f(x)在(0,1]上是增函数,所以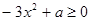
(3)对于参数a进行分类讨论得到最值。
解:(1)设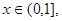 则
则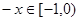 ---------1分
---------1分
所以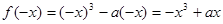 -------2分
-------2分
因为f(x)是偶函数,所以f(-x)=f(x) ----------3分
所以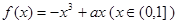 ---------4分
---------4分
(2)当 时,
时,
所以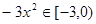
因为f(x)在(0,1]上是增函数,所以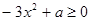 -------------6分
-------------6分
所以a的取值范围是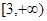 ---------7分
---------7分
(3)(i)当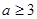 时,由(2)知f(x)在区间(0,1]上是增函数
时,由(2)知f(x)在区间(0,1]上是增函数
所以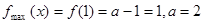 不合题意,舍去
不合题意,舍去
(ii)当 时,在区间(0,1]上,
时,在区间(0,1]上,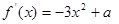
令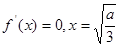 -------------8分
-------------8分
由下表
|
|
|
|
|
|
|
+ |
0 |
- |
|
|
增 |
极大值 |
减 |
f(x)在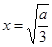 处取得最大值 ----------9分
处取得最大值 ----------9分
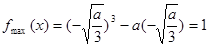 -------------10分
-------------10分
所以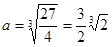 --------11分
--------11分
注意到 ,所以
,所以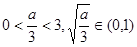 符合题意 --------12分
符合题意 --------12分
(iii)当 时,在区间(0,1]上,
时,在区间(0,1]上, ,
,
所以f(x)为减函数,无最大值 --------13分
综上所述,存在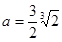 使得当
使得当 时,f(x)有最大值1、
时,f(x)有最大值1、


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x)+f(-x) |
| 2 |
| f(x)-f(-x) |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:《第1章 集合与函数概念》2010年单元测试卷2(大纲版)(解析版) 题型:解答题
 ,
,
查看答案和解析>>
科目:高中数学 来源:2015届福建省高一上学期第一次月考数学试卷(解析版) 题型:解答题
设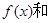
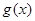 是定义在R上的两个函数,
是定义在R上的两个函数,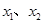 是R上任意两个不等的实根,设
是R上任意两个不等的实根,设
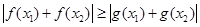 恒成立,且
恒成立,且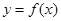 为奇函数,判断函数
为奇函数,判断函数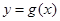 的奇偶性并说明理由。
的奇偶性并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com