
(本题满分12分)
如图,四面体ABCD中,O、E分别是BD、BC的中点,
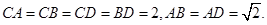
(I)求证: 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的余弦值;
(III)求点E到平面ACD的距离。

(I)证明:见解析;(II)异面直线AB与CD所成角的余弦值为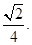 ;
;
(III)点E到平面ACD的距离为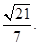
【解析】本小题主要考查直线与平面的位置关系、异面直线所成的角以及点到平面的距离基本知识,考查空间想象能力、逻辑思维能力和运算能力.
(I)欲证AO⊥平面BCD,根据直线与平面垂直的判定定理可知只需证AO与平面BCD内两相交直线垂直,而CO⊥BD,AO⊥OC,BD∩OC=O,满足定理;
(II)以O为原点,OB为x轴,OC为y轴,OA为z轴,建立空间直角坐标系,异面直线AB与CD的向量坐标,求出两向量的夹角即可;
(III)求出平面ACD的法向量,点E到平面ACD的距离转化成向量EC在平面ACD法向量上的投影即可.
(I)证明:连结OC
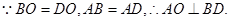
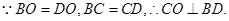
在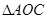 中,由已知可得
中,由已知可得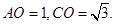
而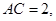
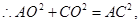
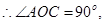 即
即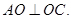
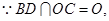
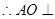 平面
平面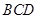
(II)解:取AC的中点M,连结OM、ME、OE,由E为BC的中点知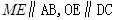
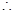 直线OE与EM所成的锐角就是异面直线AB与CD所成的角
直线OE与EM所成的锐角就是异面直线AB与CD所成的角
在 中,
中,
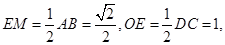
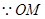 是直角
是直角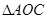 斜边AC上的中线,
斜边AC上的中线,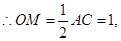
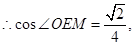
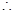 异面直线AB与CD所成角的余弦值为
异面直线AB与CD所成角的余弦值为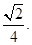
(III)解:设点E到平面ACD的距离为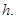
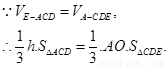 在
在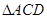 中,
中,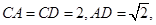
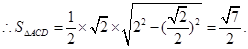 而
而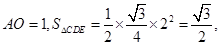
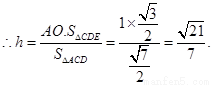
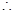 点E到平面ACD的距离为
点E到平面ACD的距离为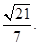


科目:高中数学 来源:2015届湖北武汉部分重点中学高一上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分12分)生物体死亡后,它机体内原有的碳14会按确定的规律衰减,大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.
(Ⅰ)设生物体死亡时体内每克组织中的碳14的含量为1,根据上述规律,写出生物体内碳14的含量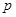 与死亡年数
与死亡年数 之间的函数关系式;
之间的函数关系式;
(Ⅱ)湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7℅,试推算马王堆汉墓的年代.(精确到个位;辅助数据: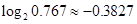 )
)
查看答案和解析>>
科目:高中数学 来源:2014届重庆市高二上学期10月月考考理科数学试卷(解析版) 题型:解答题
(本题满分12分)
如图,已知 内接于圆
内接于圆 ,
, 是圆
是圆 的直径,四边形
的直径,四边形 为平行四边形,
为平行四边形,
 平面
平面 ,
, ,
, 。
。
⑴证明: DE⊥平面ADC;
⑵记 求三棱锥
求三棱锥 的体积
的体积 ;
;
⑶当 取得最大值时,求证:
取得最大值时,求证: 。
。

查看答案和解析>>
科目:高中数学 来源:2014届重庆市高二上学期10月月考考理科数学试卷(解析版) 题型:解答题
(本题满分12分)
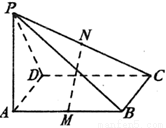
如图,PA⊥矩形ABCD所在的平面,M、N分别是AB、PC的中点.
(1)求证:MN//平面PAD
(2)求证:MN⊥CD
(3)若∠PDA=45°,求证:MN⊥平面PCD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com