
【题目】已知函数![]() .
.
(1)判断并证明函数![]() 的奇偶性;
的奇偶性;
(2)判断当![]() 时函数
时函数![]() 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)若![]() 定义域为
定义域为![]() ,解不等式
,解不等式![]() .
.
【答案】(1)奇函数(2)增函数(3)![]()
【解析】试题分析:(1)判断与证明函数的奇偶性,首先要确定函数的定义域是否关于原点对称,再判断f(-x)与f(x)的关系,如果对定义域上的任意x,都满足f(-x)=f(x)就是偶函数,如果f(-x)=-f(x)就是奇函数,否则是非奇非偶函数。(2)利函数单调性定义证明单调性,按假设,作差,化简,判断,下结论五个步骤。(3)由(1)(2)奇函数![]() 在(-1,1)为单调函数,
在(-1,1)为单调函数,
原不等式变形为f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函数的单调性及定义(-1,1)求解得x范围。
试题解析:(1)函数![]() 为奇函数.证明如下:
为奇函数.证明如下:
![]() 定义域为
定义域为![]()
又![]()
![]() 为奇函数
为奇函数
(2)函数![]() 在(-1,1)为单调函数.证明如下:
在(-1,1)为单调函数.证明如下:
任取![]() ,则
,则
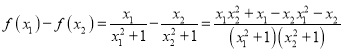
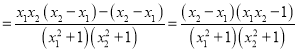
![]()
![]() ,
, ![]()
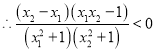
即![]()
故![]() 在(-1,1)上为增函数
在(-1,1)上为增函数
(3)由(1)、(2)可得
![]() 则
则
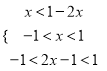 解得:
解得: ![]()
所以,原不等式的解集为![]()


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
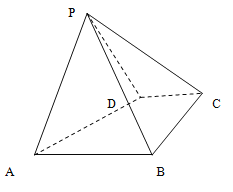
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,侧面
,侧面![]() 底面
底面![]() ,且
,且![]() 是以
是以![]() 为底的等腰三角形.
为底的等腰三角形.
(Ⅰ)证明:![]()
(Ⅱ)若四棱锥![]() 的体积等于
的体积等于![]() .问:是否存在过点
.问:是否存在过点![]() 的平面
的平面![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列5个命题中正确命题的个数是( )
①对于命题p:x∈R,使得x2+x+1<0,则綈p:x∈R,均有x2+x+1>0;
②m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
③已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则线性回归方程为![]() =1.23x+0.08;
=1.23x+0.08;
④若实数x,y∈[-1,1],则满足x2+y2≥1的概率为![]() ;
;
⑤曲线y=x2与y=x所围成图形的面积是S= (x-x2)dx.
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆上的点,直线
是椭圆上的点,直线![]() 与
与![]() (
(![]() 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为![]() .若动点
.若动点![]() 满足
满足![]() ,试探究是否存在两个定点
,试探究是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节吃粽子是我国的传统习俗.设一盘中装有10个粽子,其中豆沙粽2个,肉粽3个,白粽5个,这三种粽子的外观完全相同.从中任意选取3个.
(1)求三种粽子各取到1个的概率;
(2)设X表示取到的豆沙粽个数,求X的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy上取两个定点![]() 再取两个动点
再取两个动点![]() ,
,![]() ,且
,且![]() .
.
(Ⅰ)求直线![]() 与
与![]() 交点M的轨迹C的方程;
交点M的轨迹C的方程;
(Ⅱ)过![]() 的直线与轨迹C交于P,Q,过P作
的直线与轨迹C交于P,Q,过P作![]() 轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若
轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(![]() ,简称
,简称![]() )是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为
)是定量描述空气质量状况的无量纲指数,参与空气质量评价的主要污染物为![]() 等六项.空气质量按照
等六项.空气质量按照![]() 大小分为六级:一级
大小分为六级:一级![]() 为优;二级
为优;二级![]() 为良好;三级
为良好;三级![]() 为轻度污染;四级
为轻度污染;四级![]() 为中度污染;五级
为中度污染;五级![]() 为重度污染;六级
为重度污染;六级![]() 为严重污染.
为严重污染.
某人根据环境监测总站公布的数据记录了某地某月连续10天![]() 的茎叶图如图所示:
的茎叶图如图所示:

(1)利用访样本估计该地本月空气质量优良(![]() )的天数;(按这个月总共30天计算);
)的天数;(按这个月总共30天计算);
(2)若从样本中的空气质量不佳(![]() )的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率.
)的这些天中,随机地抽取三天深入分析各种污染指标,求这三天的空气质量等级互不相同的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com