
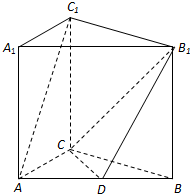
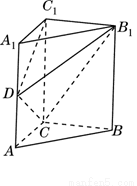
 如图,在直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.
如图,在直三棱柱(侧棱垂直于底面)ABC-A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点.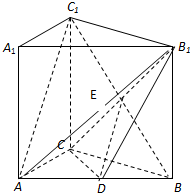 解:(1)连结AB1,由已知可得CB∥C1B1,CB=C1B1
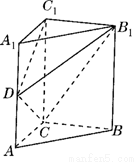
解:(1)连结AB1,由已知可得CB∥C1B1,CB=C1B1| x2+9 |
| x2+25 |


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
 (2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线.
(2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线.3
| ||
| 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线.
(2013•成都二模)如图,在直三棱柱(侧棱与底面垂直的三棱柱)ABC-A1B1C1中,AC=AA1=2AB=2,∠BAC=90°,点D是侧棱CC1 延长线上一点,EF是平面ABD与平面A1B1C1的交线.
| ||
| 26 |
查看答案和解析>>
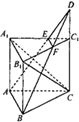
科目:高中数学 来源:2012-2013学年贵州黔东南州高三第二次模拟(5月)考试理科数学试卷(解析版) 题型:解答题
如图,在直三棱柱(即侧棱与底面垂直的三棱柱) 中,
中,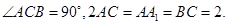
(I)若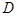 为
为 的中点,求证:平面
的中点,求证:平面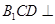 平面
平面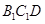 ;
;
(II)若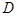 为线段
为线段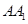 上一点,且二面角
上一点,且二面角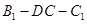 的大小为
的大小为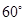 ,试确定
,试确定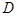 的位置.
的位置.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年贵州黔东南州高三第二次模拟(5月)考试文科数学试卷(解析版) 题型:解答题
如图,在直三棱柱(即侧棱与底面垂直的三棱柱)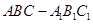 中,
中,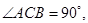
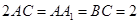 ,
,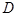 为
为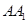 的中点
的中点
(I)求证:平面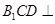 平面
平面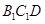 ;
;
(II)求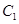 到平面
到平面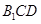 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com