
【题目】已知函数![]() .
.
(1)函数![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)函数![]() (
(![]() )的图象在点
)的图象在点![]() 处的切线为
处的切线为![]() ,证明:有且只有两个点
,证明:有且只有两个点![]() 使得直线
使得直线![]() 与函数
与函数![]() 的图象也相切.
的图象也相切.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(2)证明见解析.
上单调递增;(2)证明见解析.
【解析】
(1)先对![]() 求导,然后对a分类讨论,求出单调区间即可;
求导,然后对a分类讨论,求出单调区间即可;
(2)设![]() (
(![]() ),可求出直线
),可求出直线![]() 的方程为:
的方程为:![]() ,假设直线
,假设直线![]() 与
与![]() 的图象也相切,切点为
的图象也相切,切点为![]() ,所以直线
,所以直线![]() 的方程也可以写作为:
的方程也可以写作为:![]() ,又因为斜率相等可得
,又因为斜率相等可得![]() ,即
,即![]() ,由此可得
,由此可得![]() ,令
,令![]() (
(![]() ),然后结合零点存在性定理证明即可.
),然后结合零点存在性定理证明即可.
(1)![]() (
(![]() ),所以
),所以![]() ,
,
①当![]() 即
即![]() 时:
时:![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 即
即![]() 时:令
时:令![]() 有:
有:![]() ,
,
所以:![]() 在
在![]() 单调递减,在
单调递减,在![]() 上单调递增;
上单调递增;
(2)设![]() (
(![]() ),
),
![]() ,所以:
,所以:![]() ,
,
所以直线![]() 的方程为:
的方程为:![]() ,即:
,即:![]() ,①
,①
假设直线![]() 与
与![]() 的图象也相切,切点为
的图象也相切,切点为![]() ,
,
因为![]() ,所以:
,所以:![]() ,
,
所以直线![]() 的方程也可以写作为:
的方程也可以写作为:![]() ,
,
又因为![]() ,即:
,即:![]() ,
,
所以直线![]() 的方程为:
的方程为: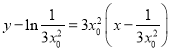 ,即:
,即:![]() ,②
,②
由①②有:![]() ,即:
,即:![]() ,
,
令![]() (
(![]() ),
),
所以![]() ,
,
令![]() ,得:
,得:![]() ,
,
所以:![]() 在
在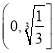 上单调递减,在
上单调递减,在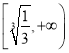 上单调递增,
上单调递增,
所以: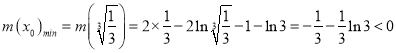 ,
,
又因为:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以:![]() 在
在![]() 有且只有两个实数根,
有且只有两个实数根,
所以有且只有两个点![]() 使得直线
使得直线![]() 与函数
与函数![]() 的图象也相切.
的图象也相切.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的普通方程;
的普通方程;
(2)设![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冠状病毒是一个大型病毒家族,己知可引起感冒以及中东呼吸综合征(MERS)和严重急性呼吸综合征(SARS)等较严重疾病.而今年出现的新型冠状病毒(nCoV)是以前从未在人体中发现的冠状病毒新毒株.人感染了新型冠状病毒后常见体征有呼吸道症状、发热、咳嗽、气促和呼吸困难等.在较严重病例中,感染可导致肺炎、严重急性呼吸综合征、肾衰竭,甚至死亡.某医院为筛查冠状病毒,需要检验血液是否为阳性,现有![]() 份需检验血液.
份需检验血液.
(1)假设这![]() 份需检验血液有且只有一份为阳性,从中依次不放回的抽取
份需检验血液有且只有一份为阳性,从中依次不放回的抽取![]() 份血液,已知前两次的血液均为阴性,求第
份血液,已知前两次的血液均为阴性,求第![]() 次出现阳性血液的概率;
次出现阳性血液的概率;
(2)现在对![]() 份血液进行检验,假设每份血液的检验结果是阳性还是阴性都是独立的,据统计每份血液是阳性结果的概率为
份血液进行检验,假设每份血液的检验结果是阳性还是阴性都是独立的,据统计每份血液是阳性结果的概率为![]() ,现在有以下两种检验方式:方式一:逐份检验;方式二:混合检验,将
,现在有以下两种检验方式:方式一:逐份检验;方式二:混合检验,将![]() 份血液分别取样混合在一起检验(假设血液混合后不影响血液的检验).若检验结果为阴性,则这
份血液分别取样混合在一起检验(假设血液混合后不影响血液的检验).若检验结果为阴性,则这![]() 份血液全为阴性,检验结束;如果检验结果为阳性,则这
份血液全为阴性,检验结束;如果检验结果为阳性,则这![]() 份血液中有为阳性的血液,为了明确这
份血液中有为阳性的血液,为了明确这![]() 份血液究竟哪几份为阳性,就要对这
份血液究竟哪几份为阳性,就要对这![]() 份再逐份检验.从检验的次数分析,哪一种检验方式更好一些,并说明理由.参考数据:
份再逐份检验.从检验的次数分析,哪一种检验方式更好一些,并说明理由.参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:![]() ,直线l:
,直线l:![]() (
(![]() )过定点N,点P是圆M上的任意一点,线段
)过定点N,点P是圆M上的任意一点,线段![]() 的垂直平分线和
的垂直平分线和![]() 相交于点Q,当点P在圆M上运动时,点Q的轨迹为曲线C.
相交于点Q,当点P在圆M上运动时,点Q的轨迹为曲线C.
(1)求曲线C的方程;
(2)直线l交C于A,B两点,D,B关于x轴对称,直线![]() 与x轴交于点E,且点D为线段
与x轴交于点E,且点D为线段![]() 的中点,求直线l的方程.
的中点,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为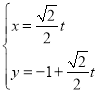 (t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为
(t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设P(0,-1),直线l与C的交点为M,N,线段MN的中点为Q,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
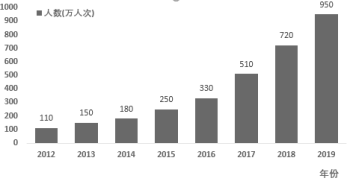
【题目】近年来,某市立足本地丰厚的文化旅游资源,以建设文化旅游强市,创建国家全域旅游示范市为引领,坚持以农为本,以乡为魂,以旅促农,多元化推动产业化发展,文化和旅游扶贪工作卓有成效,精准扶贫稳步推进.该市旅游局为了更好的了解每年乡村游人数的变化情况,绘制了如图所示的柱状图.则下列说法错误的是( )
0
A.乡村游人数逐年上升
B.相比于前一年,2015年乡村游人数增长率大于2014年乡村游人数增长率
C.近8年乡村游人数的平均数小于2016年乡村游人数
D.从2016年开始,乡村游人数明显增多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蛋糕店制作并销售一款蛋糕,制作一个蛋糕成本4元,且以9元的价格出售,若当天卖不完,剩下的则无偿捐献给饲料加工厂.根据以往100天的资料统计,得到如表需求量表:
需求量/个 | [100,110) | [110,120) | [120,130) | [130,140) | [140,150] |
天数 | 15 | 25 | 30 | 20 | 10 |
该蛋糕店一天制作了这款蛋糕X(X∈N)个,以x(单位:个,100≤x≤150,x∈N)表示当天的市场需求量,T(单位:元)表示当天出售这款蛋糕获得的利润.
(1)当x=135时,若X=130时获得的利润为T1,X=140时获得的利润为T2,试比较T1和T2的大小;
(2)当X=130时,根据上表,从利润T不少于560元的天数中,按需求量分层抽样抽取6天.
(i)求此时利润T关于市场需求量x的函数解析式,并求这6天中利润为650元的天数;
(ii)再从这6天中抽取3天做进一步分析,设这3天中利润为650元的天数为ξ,求随机变量ξ的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com