
(12分)如图,长方体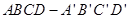 中,
中, ,
,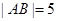 ,
,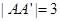 ,设E为
,设E为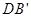 的中点,F为
的中点,F为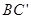 的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D,
的中点,在给定的空间直角坐标系D-xyz下,试写出A,B,C,D, ,
,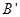 ,
,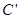 ,
,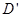 ,E,F各点的坐标.
,E,F各点的坐标.
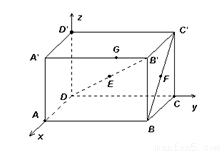
A(3,0,0),B(3,5,0),C(0,5,0),D(0,0,0); (3,0,3),
(3,0,3), (3,5,3),
(3,5,3), (0,5,3),
(0,5,3),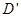 (0,0,3); E(
(0,0,3); E(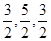 );F(
);F(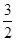 ,5,
,5,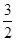 )。
)。
【解析】
试题分析:解:设原点为O,因为A,B,C,D这4个点都在坐标平面
xOy内,它们的竖坐标都是0,而它们的横坐标和纵坐标可利用 ,
,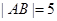 写出,所以
A(3,0,0),B(3,5,0),C(0,5,0),D(0,0,0);
写出,所以
A(3,0,0),B(3,5,0),C(0,5,0),D(0,0,0);
因为平面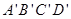 与坐标平面xOy平行,且
与坐标平面xOy平行,且 ,所以A',B',
,所以A',B',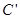 ,D'的竖坐标都是3,而它们的横坐标和纵坐标分别与A,B,C,D的相同,所以
,D'的竖坐标都是3,而它们的横坐标和纵坐标分别与A,B,C,D的相同,所以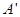 (3,0,3),
(3,0,3),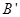 (3,5,3),
(3,5,3),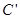 (0,5,3),
(0,5,3),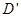 (0,0,3);由于E分别是
(0,0,3);由于E分别是 中点,所以它在坐标平面xOy上的射影为DB的中点,从而E的横坐标和纵坐标分别是
中点,所以它在坐标平面xOy上的射影为DB的中点,从而E的横坐标和纵坐标分别是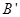 的
的 ,同理E的竖坐标也是
,同理E的竖坐标也是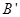 的竖坐标的
的竖坐标的 ,所以E(
,所以E(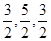 );
);
由F为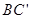 中点可知,F在坐标平面xOy的射影为BC中点,横坐标和纵坐标分别为
中点可知,F在坐标平面xOy的射影为BC中点,横坐标和纵坐标分别为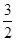 和5,同理点F在z轴上的投影是AA'中点,故其竖坐标为
和5,同理点F在z轴上的投影是AA'中点,故其竖坐标为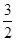 ,所以F(
,所以F(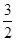 ,5,
,5,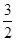 ).
).
考点:本题主要考查空间直角坐标系的概念及其应用。
点评:根据几何体的特征,在直角坐标系中,写出点的坐标。


科目:高中数学 来源: 题型:
 在如图的长方体中,AD=AA1=1,AB=2,点E在棱AB上移动.
在如图的长方体中,AD=AA1=1,AB=2,点E在棱AB上移动.| π | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
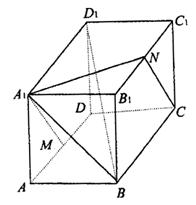
(08年潍坊市二模)(12分)如图,长方体![]() 中,
中,![]() ,
,![]() ,M是AD中点,N是
,M是AD中点,N是![]() 中点.
中点.
(1)求证:![]() 、M、C、N四点共面;
、M、C、N四点共面;
(2)求证:![]() ;
;
(3)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(4)求![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省高三上学期期中考试理科数学试卷(解析版) 题型:解答题
如图,长方体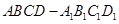 中
中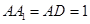 ,
,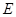 为
为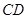 中点.
中点.
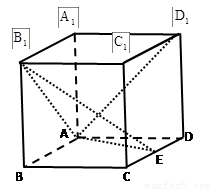
(1)求证: ;
;
(2)在棱上是否存在一点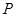 ,使得
,使得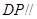 平面
平面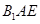 ?若存在,求
?若存在,求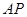 的长;若不存在,说明理由;
的长;若不存在,说明理由;
(3)若二面角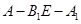 的大小为
的大小为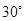 ,求
,求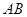 的长.
的长.
查看答案和解析>>
科目:高中数学 来源:2014届四川省高三开学检测文科数学试卷(解析版) 题型:解答题
(12分)如图,在长方体 中,
中,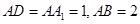 ,点E为AB的中点.
,点E为AB的中点.

(Ⅰ)求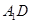 与平面
与平面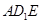 所成的角;
所成的角;
(Ⅱ)求二面角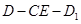 的平面角的正切值.
的平面角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com