分析:(1)由三视图即可得出:AD⊥底面CBD,AD=2,底面△BCD为等腰直角三角形,∠CBD=90°,BC=BD=1,即可求出体积;
(2)过D点作DE⊥AB交AB于E,根据条件只要证明:DE即为点D到平面ABC的距离,进而求出即可.
(3)过点D作DF⊥AC交AC于点F,连接EF,证明∠DFE即为二面角的平面角并求出即可.
解答:解:(1)由三视图可知:AD⊥底面CBD,AD=2,底面△BCD为等腰直角三角形,∠CBD=90°,BC=BD=1.
∴V
三棱锥A-BCD=
S△BCD×AD=
××12×2=
;
(2)过D点D作DE⊥AB交AB于E,
由(1)可知:AD⊥平面BCD,∴AD⊥BC,

又BC⊥BD,AD∩BD=D,
∴BC⊥平面ABD,∴BC⊥DE.
∵AB∩BC=B,∴DE⊥平面ABC.
∴DE即为点D到平面ABC的距离.
在Rt△ABD中,
DE==
=
.
(3)过点D作DF⊥AC交AC于点F,连接EF.
由(1)可知:DE⊥平面ABC.
∴DF⊥AC.
则∠DFE即为二面角的平面角.
在Rt△ADC中,由勾股定理可得AC=
=
.
∴DF=
=
=
.
在Rt△DEF中,sin∠DFE=
=
=
.
点评:由三视图正确得到原几何体的位置关系,熟练掌握线面垂直的判定和性质定理及二面角的求法是解题的关键.

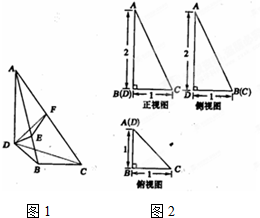 已知三棱锥A-BCD及其三视图如图所示.
已知三棱锥A-BCD及其三视图如图所示.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案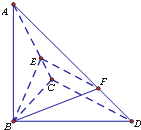 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且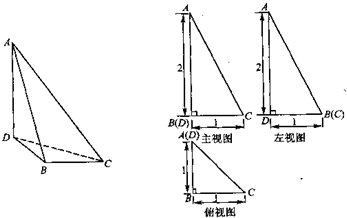 (2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.
(2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.