解:(1)函数f (x)在区间(0,+∞)上,证明如下:
∵f(x)=
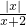
,
∴当x>0时,f(x)=

∵

上是减函数
∴f (x)在区间(0,+∞)上是增函数.(4分)
(2)原方程即:
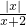
=kx
2①
①由方程的形式可以看出,x=0恒为方程①的一个解.(5分)
②当x<0且x≠-2时方程①有解,则
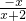
=kx
2即kx
2+2kx+1=0
当k=0时,方程kx
2+2kx+1=0无解;
当k≠0时,△=4k
2-4k≥0即k<0或k≥1时,方程kx
2+2kx+1=0有解.
设方程kx
2+2kx+1=0的两个根分别是x
1,x
2则x
1+x
2=-2,x
1x
2=

.
当k>1时,方程kx
2+2kx+1=0有两个不等的负根;
当k=1时,方程kx
2+2kx+1=0有两个相等的负根;
当k<0时,方程kx
2+2kx+1=0有一个负根(8分)
③当x>0时,方程①有解,则

=kx
2,kx
2+2kx-1=0
当k=0时,方程kx
2+2kx-1=0无解;
当k≠0时,,△=4k
2+4k≥0即k>0或k≤-1时,方程kx
2+2kx-1=0有解.
设方程kx
2+2kx-1=0的两个根分别是x
3,x
4∴x
3+x
4=-2,x
3x
4=-

∴当k>0时,方程kx
2+2kx-1=0有一个正根,
当k≤-1时,方程kx
2+2kx+1=0没有正根.(11分).
综上可得,当k∈(1,+∞)时,方程f (x)=kx
2有四个不同的实数解.(13分).
分析:(1)判断函数f (x)在区间(0,+∞)上的单调性,并加以证明,先去绝对值号对函数表达式化简,根据其形式判断出函数的性质,再进行证明
(2)方程f (x)=kx
2有四个不同的实数解,代入函数表达式,进行探究,由于方程带有绝对值,故需要分类去绝对值,在每一类中找出满足方程有两解的参数的值,合并既得.
点评:本题第一问考查单调性的判断,题目较易,第二问由方程有四个解来求参数的范围,本题对思维的严密性要求很高,需要熟练运用分类讨论的思想,因为题目中有太多的不确定性,本题难度较大.

 .
.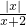 ,
,
 上是减函数
上是减函数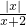 =kx2①
=kx2①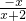 =kx2即kx2+2kx+1=0
=kx2即kx2+2kx+1=0 .
. =kx2,kx2+2kx-1=0
=kx2,kx2+2kx-1=0

