
【题目】以平面直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 绕极点逆时针旋转
绕极点逆时针旋转![]() 后得到曲线
后得到曲线![]() .
.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() :
:![]() 与
与![]() ,
,![]() 分别相交于异于极点的
分别相交于异于极点的![]() ,
,![]() 两点,求
两点,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】如果某企业每月生猪的死亡率不超过百分之一,则该企业考核为优秀.现获得某企业2019年1月到8月的相关数据如下表所示:
月份 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 |
月养殖量/千只 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 12 |
月利润/十万元 | 3.6 | 4.1 | 4.4 | 5.2 | 6.2 | 7.5 | 7.9 | 9.1 |
生猪死亡数最/只 | 29 | 37 | 49 | 53 | 77 | 98 | 126 | 145 |
(1)求出月利润;y(十万元)关于月养殖量x(千只)的线性回归方程(精确到0.01);
(2)若2019年9月份该企业月养殖量为1.4万只,请你预估该月月利润是多少万元;
(3)从该企业2019年1月到8月这8个月中任意选取3个月,用X表示3个月中该企业考核获得优秀的个数,求X的分布列和数学期望./p>
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
附:线性回归方程![]() 中,
中,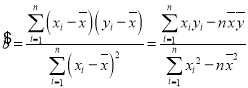 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,上顶点为A,右顶点为B.点
,上顶点为A,右顶点为B.点![]() 在椭圆C内,且直线
在椭圆C内,且直线![]() 与直线
与直线![]() 垂直.
垂直.
(1)求C的方程;
(2)设过点P的直线交C于M,N两点,求证:以![]() 为直径的圆过点
为直径的圆过点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
,![]() ,若
,若![]() ,
,![]() 的方向是沿
的方向是沿![]() 方向绕着
方向绕着![]() 点按逆时针方向旋转
点按逆时针方向旋转![]() 角得到的,则称
角得到的,则称![]() 经过一次
经过一次![]() 变换得到
变换得到![]() .已知向量
.已知向量![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,
,![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,…,如此下去,
,…,如此下去,![]() 经过一次
经过一次![]() 变换后得到
变换后得到![]() ,设
,设![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x22(a+2)x+a2,g(x)=x2+2(a2)xa2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则AB=( )
A.a22a16B.a2+2a16
C.16D.16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“![]() ”表示一个阳爻,“
”表示一个阳爻,“![]() ”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )
”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】法国的数学家费马(PierredeFermat)曾在一本数学书的空白处写下一个看起来很简单的猜想:当整数![]() 时,找不到满足
时,找不到满足![]() 的正整数解.该定理史称费马最后定理,也被称为费马大定理.费马只是留下这个叙述并且说他已经发现这个定理的证明妙法,只是书页的空白处不够无法写下.费马也因此为数学界留下了一个千古的难题,历经数代数学家们的努力,这个难题直到1993年才由我国的数学家毛桂成完美解决,最终证明了费马大定理的正确性.现任取
的正整数解.该定理史称费马最后定理,也被称为费马大定理.费马只是留下这个叙述并且说他已经发现这个定理的证明妙法,只是书页的空白处不够无法写下.费马也因此为数学界留下了一个千古的难题,历经数代数学家们的努力,这个难题直到1993年才由我国的数学家毛桂成完美解决,最终证明了费马大定理的正确性.现任取![]() ,则等式
,则等式![]() 成立的概率为( )
成立的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
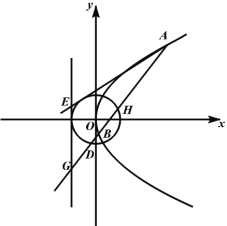
【题目】如图,在平面直角系![]() 中,点A为曲线C:
中,点A为曲线C:![]() 在第一象限的图象上的动点,点E,G在曲线C的准线
在第一象限的图象上的动点,点E,G在曲线C的准线![]() 上,且点G在x轴的下方,圆O与准线相切,直线
上,且点G在x轴的下方,圆O与准线相切,直线![]() 交曲线C于点B,交圆O于点D,H.
交曲线C于点B,交圆O于点D,H.
(1)当点H为曲线C的焦点,![]() 时,求
时,求![]() ;
;
(2)当点O为![]() 的内心时,若
的内心时,若![]() ,求点A的坐标.
,求点A的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com