分析:由直线方程的特点得到此直线恒过A(2,4),由曲线方程的特点得到曲线为一个半圆,在平面直角坐标系中画出相应的图形,根据直线与半圆有2个交点,取两个特殊情况:当直线与半圆相切,且切点在第二象限时,可得出圆心到直线的距离等于圆的半径,即d=r,利用点到直线的距离公式列出关于k的方程,求出方程的解得到此时k的值;当直线过点C时,将C的坐标代入直线方程,得到关于k的方程,求出方程的解得到此时k的值,由图象可得出满足题意k的取值范围.
解答:解:直线y=k(x-2)+4,
当x=2时,y=4,可得此直线恒过A(2,4),
曲线
y=为圆心在坐标原点,半径为2的半圆,
根据题意作出相应的图形,如图所示:
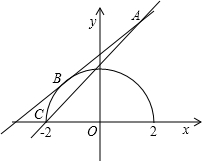
当直线y=k(x-2)+4与半圆相切(切点在第二象限)时,圆心到直线的距离d=r,
∴
=2,即4k
2-16k+16=4+4k
2,
解得:k=
,
当直线y=k(x-2)+4过点C时,将x=-2,y=0代入直线方程得:-4k+4=0,
解得:k=1,
则直线与曲线有2个交点时k的范围为(
,1].
故答案为:(
,1]
点评:此题考查了直线与圆的位置关系,利用了数形结合的数学思想,直线与圆的位置关系由d与r的大小来判断(d为圆心到直线的距离,r为圆的半径),当d>r时,直线与圆相离;当d=r时,直线与圆相切;当d<r时,直线与圆相交.



