
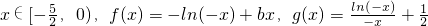 .
.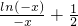
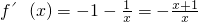 ,当x∈(-
,当x∈(- ,-1)时,f′(x)<0,当x∈(-1,0)时,f′(x)>0
,-1)时,f′(x)<0,当x∈(-1,0)时,f′(x)>0 ,-1)时,单调递减;在x∈(-1,0)时,单调递增
,-1)时,单调递减;在x∈(-1,0)时,单调递增 ,当x∈[-
,当x∈[- ,0)时,g′(x)<0,g(x)单调递减,g(x)的最大值为
,0)时,g′(x)<0,g(x)单调递减,g(x)的最大值为
 ,0),f′(x)=b-
,0),f′(x)=b- =
=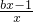
 >0,∴f(x)min=f(-
>0,∴f(x)min=f(- )=
)=
 >0,,∴f(x)min=f(-
>0,,∴f(x)min=f(- )=-
)=-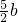

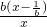
 ,即
,即 时,f′(x)=b-
时,f′(x)=b- ≥0,
≥0, )=-
)=-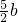

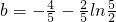

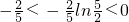
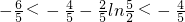 ,不满足
,不满足


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源:2012-2013学年浙江省宁波四中高三(上)期中数学试卷(理科)(解析版) 题型:解答题
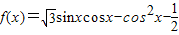
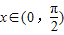 ,求f(x)的值域;
,求f(x)的值域;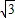 ,f(C)=0,若向量
,f(C)=0,若向量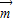 =(1,sinA)与向量
=(1,sinA)与向量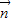 =(2,sinB)共线,求a,b的值.
=(2,sinB)共线,求a,b的值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省淮安市盱眙县马坝中学高三(上)第二次月考数学试卷(解析版) 题型:解答题

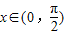 ,求f(x)的值域;
,求f(x)的值域; ,f(C)=0,若向量
,f(C)=0,若向量 =(1,sinA)与向量
=(1,sinA)与向量 =(2,sinB)共线,求a,b的值.
=(2,sinB)共线,求a,b的值.查看答案和解析>>
科目:高中数学 来源:2012-2013学年浙江省宁波四中高三(上)期中数学试卷(理科)(解析版) 题型:解答题

 ,求f(x)的值域;
,求f(x)的值域; ,f(C)=0,若向量
,f(C)=0,若向量 =(1,sinA)与向量
=(1,sinA)与向量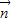 =(2,sinB)共线,求a,b的值.
=(2,sinB)共线,求a,b的值.查看答案和解析>>
科目:高中数学 来源:2012年新疆高考第二次适应性检测数学试卷(理科)(解析版) 题型:解答题
 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com