
(本小题满分13分)已知椭圆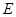 的中心在原点
的中心在原点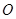 ,焦点
,焦点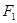 ,
,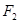 在
在 轴上,经过点
轴上,经过点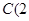 ,
,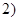 ,且抛物线
,且抛物线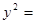
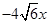 的焦点为
的焦点为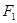 .
.
(1) 求椭圆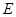 的方程;
的方程;
(2) 垂直于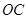 的直线
的直线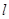 与椭圆
与椭圆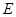 交于
交于 ,
, 两点,当以
两点,当以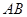 为直径的圆
为直径的圆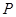 与
与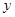 轴相切时,求直线
轴相切时,求直线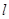 的方程和圆
的方程和圆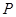 的方程.
的方程.
(1)
(2)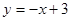 ,
,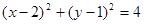 或
或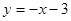 ,
,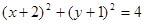
解析试题分析:(1) 设椭圆 的方程为
的方程为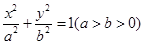 ,
,
则由椭圆经过点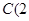 ,
,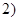 ,有
,有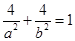 ,①
,①
∵抛物线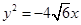 的焦点为
的焦点为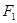 ,∴
,∴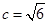 , ②
, ②
又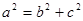 ③,
③,
由①、②、③得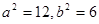 ,
,
所以椭圆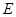 的方程为
的方程为 . ……5分
. ……5分
(2) 依题意,直线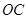 斜率为1,
斜率为1,
由此设直线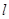 的方程为
的方程为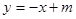 ,代入椭圆
,代入椭圆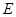 方程,得
方程,得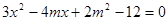 .
.
由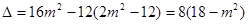 ,得
,得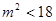 .
.
记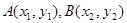 ,
,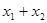 =
= ,
,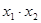 =
=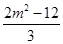 ,
,
圆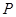 的圆心为
的圆心为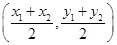 ,即
,即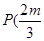 ,
, 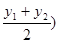 ,
,
半径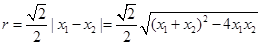
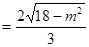 ,
,
当圆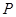 与
与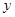 轴相切时,
轴相切时,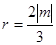
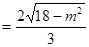 ,即
,即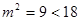 ,
,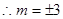 ,
,
当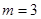 时,直线
时,直线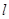 方程为
方程为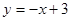 ,此时,
,此时,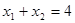 ,圆心为(2,1),半径为2,圆
,圆心为(2,1),半径为2,圆 的方程为
的方程为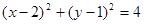 ;
;
同理,当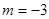 时,直线
时,直线 方程为
方程为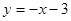 ,
,
圆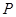 的方程为
的方程为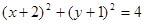 . ……13分
. ……13分
考点:本小题主要考查椭圆与抛物线基本量之间的关系和椭圆标准方程的求解、直线与椭圆的位置关系、韦达定理、直线与圆的位置关系、直线与圆的方程的求解,考查了学生综合运算所学知识分析问题、解决问题的能力和数形结合数学思想的应用以及运算求解能力.
点评:每年高考圆锥曲线问题都出现在压轴题的位置上,难度一般较大,要充分利用数形结合数学思想方法,尽可能的寻求简单方法,尽可能的减少运算,另外思维一定要严谨,运算一定要准确.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(12分)如图所示,椭圆C: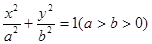 的离心率
的离心率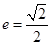 ,左焦点为
,左焦点为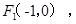 右焦点为
右焦点为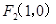 ,短轴两个端点为
,短轴两个端点为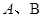 .与
.与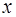 轴不垂直的直线
轴不垂直的直线 与椭圆C交于不同的两点
与椭圆C交于不同的两点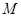 、
、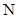 ,记直线
,记直线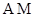 、
、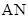 的斜率分别为
的斜率分别为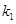 、
、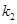 ,且
,且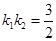 .
.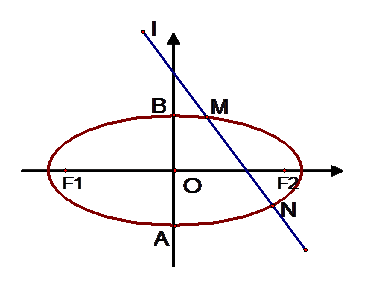
(1)求椭圆 的方程;
的方程;
(2)求证直线 与
与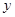 轴相交于定点,并求出定点坐标.
轴相交于定点,并求出定点坐标.
(3)当弦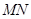 的中点
的中点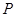 落在
落在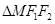 内(包括边界)时,求直线
内(包括边界)时,求直线 的斜率的取值。
的斜率的取值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(10分)过直角坐标平面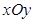 中的抛物线
中的抛物线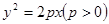 ,直线
,直线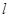 过焦点
过焦点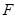 且与抛物线相交于
且与抛物线相交于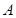 ,
,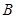 两点.
两点.
⑴当直线的倾斜角为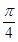 时,用
时,用 表示
表示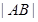 的长度;
的长度;
⑵当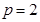 且三角形
且三角形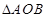 的面积为4时,求直线
的面积为4时,求直线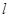 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分) 已知椭圆 的离心率
的离心率 ,A,B
,A,B
分别为椭圆的长轴和短轴的端点, 为AB的中点,O为坐标原点,且
为AB的中点,O为坐标原点,且 .
.
(1)求椭圆的方程;
(2)过(-1,0)的直线 交椭圆于P,Q两点,求△POQ面积最大时直线
交椭圆于P,Q两点,求△POQ面积最大时直线 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知椭圆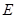 的对称轴为坐标轴,焦点在
的对称轴为坐标轴,焦点在 轴上,离心率
轴上,离心率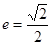 ,
,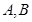 分别为椭圆的上顶点和右顶点,且
分别为椭圆的上顶点和右顶点,且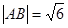 .
.
(Ⅰ)求椭圆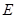 的方程;
的方程;
(Ⅱ)已知直线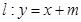 与椭圆
与椭圆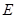 相交于
相交于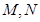 两点,且
两点,且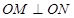 (其中
(其中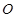 为坐标原点),求
为坐标原点),求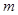 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分16分)如图,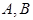 是椭圆
是椭圆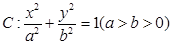 的左、右顶点,椭圆
的左、右顶点,椭圆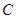 的离心率为
的离心率为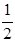 ,右准线
,右准线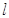 的方程为
的方程为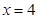 .
.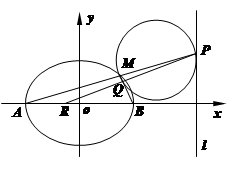
(1)求椭圆方程;
(2)设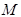 是椭圆
是椭圆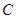 上异于
上异于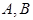 的一点,直线
的一点,直线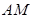 交
交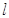 于点
于点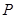 ,以
,以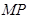 为直径的圆记为
为直径的圆记为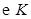 .
.
①若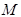 恰好是椭圆
恰好是椭圆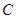 的上顶点,求
的上顶点,求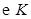 截直线
截直线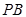 所得的弦长;
所得的弦长;
②设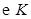 与直线
与直线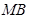 交于点
交于点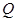 ,试证明:直线
,试证明:直线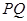 与
与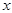 轴的交点
轴的交点 为定点,并求该定点的坐标.
为定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题10分)已知 ,动点
,动点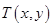 满足
满足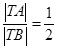 ,设动点
,设动点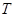 的轨迹是曲线
的轨迹是曲线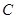 ,直线
,直线 :
: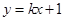 与曲线
与曲线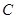 交于
交于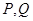 两点.(1)求曲线
两点.(1)求曲线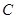 的方程;
的方程;
(2)若 ,求实数
,求实数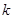 的值;
的值;
(3)过点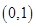 作直线
作直线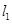 与
与 垂直,且直线
垂直,且直线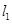 与曲线
与曲线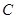 交于
交于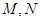 两点,求四边形
两点,求四边形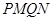 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
如图,设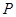 是圆
是圆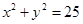 上的动点,点D是
上的动点,点D是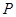 在
在 轴上的投影,M为
轴上的投影,M为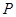 D上一点,且
D上一点,且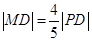
(Ⅰ)当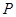 的在圆上运动时,求点M的轨迹C的方程;
的在圆上运动时,求点M的轨迹C的方程;
(Ⅱ)求过点(3,0)且斜率为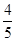 的直线被C所截线段的长度。
的直线被C所截线段的长度。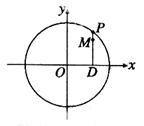
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com