
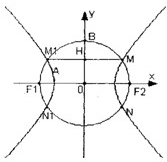
 ШчЭМF1ЃЈ-cЃЌ0ЃЉЃЌF2ЃЈcЃЌ0ЃЉЮЊЫЋЧњЯпEЕФСННЙЕуЃЌвдF1F2ЮЊжБОЖЕФдВOгыЫЋЧњЯпEНЛгкMЁЂNЁЂM1ЁЂN1ЃЌBЪЧдВOгыyжсЕФНЛЕуЃЌСЌНгMM1гыOBНЛгкHЃЌЧвHЪЧOBЕФжаЕуЃЎ
ШчЭМF1ЃЈ-cЃЌ0ЃЉЃЌF2ЃЈcЃЌ0ЃЉЮЊЫЋЧњЯпEЕФСННЙЕуЃЌвдF1F2ЮЊжБОЖЕФдВOгыЫЋЧњЯпEНЛгкMЁЂNЁЂM1ЁЂN1ЃЌBЪЧдВOгыyжсЕФНЛЕуЃЌСЌНгMM1гыOBНЛгкHЃЌЧвHЪЧOBЕФжаЕуЃЎ| F1A |
| AM |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| c |
| 2 |
| ||
| 2 |
| c |
| 2 |
| 2 |
| F1A |
| AM |
| ||
| 2 |
| c |
| 2 |
(
| ||
| 2(1+ІЫ) |
| ІЫc |
| 2(1+ІЫ) |
(
| ||
| 4(1+ІЫ)2a2 |
| ІЫ2c2 |
| 4(1+ІЫ)2b2 |
| 2 |
| c |
| a |
| c |
| b |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
|
|
| c |
| 2 |
| ||
| 2 |
| c |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
|
| 2 |
| 3 |
| 2 |
| F1A |
| AM |
| ||
| 2 |
| c |
| 2 |
(
| ||
| 2(1+ІЫ) |
| ІЫc |
| 2(1+ІЫ) |
(
| ||
| 4(1+ІЫ)2a2 |
| ІЫ2c2 |
| 4(1+ІЫ)2b2 |
| 2 |
| c |
| a |
| c |
| b |
| 2 |
| ||
| 4 |
| ||
| 4 |
| F1A |
| AM |


 ШЋФмВтПиЦкФЉаЁзДдЊЯЕСаД№АИ
ШЋФмВтПиЦкФЉаЁзДдЊЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
 ШчЭМЃЌЭждВCЃК
ШчЭМЃЌЭждВCЃК| x2 |
| a2 |
| y2 |
| b2 |
| 7 |
| AP |
| PB |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКРфЫЎНЪавЛжа2007НьИпШ§ЕкЪЎДЮФЃФтПМЪдРэПЦЪ§бЇЪдОэ ЬтаЭЃК044
ШчЭМF1(ЃcЃЌ0)F2(cЃЌ0)ЮЊЫЋЧњЯпEЕФСННЙЕуЃЌвдF1F2ЮЊжБОЖЕФдВOгыЫЋЧњЯпEНЛгкMЁЂNЁЂM1ЁЂN1ЃЌBЪЧдВOгыyжсЕФНЛЕуЃЌСЌНгMM1гыOBНЛгкHЃЌЧвHЪЧOBЕФжаЕуЃЌ

(1)ЕБcЃН1ЪБЃЌЧѓЫЋЧњЯпEЕФЗНГЬЃЛ(4Зж)
(2)ЪджЄЃКЖдШЮвтЕФе§ЪЕЪ§cЃЌЫЋЧњЯпEЕФРыаФТЪЮЊГЃЪ§ЃЛ(4Зж)
(3)СЌНгF1MгыЫЋЧњЯпEНЛгкЕуAЃЌЪЧЗёДцдкГЃЪ§![]() КуГЩСЂЃЌШєДцдкЪдЧѓГіІЫЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ(5Зж)
КуГЩСЂЃЌШєДцдкЪдЧѓГіІЫЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ(5Зж)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКНЫеЪЁГЃжнИпМЖжабЇ2007ЁЋ2008бЇФъЕкШ§ДЮНзЖЮНЬбЇжЪСПЕїбаИпШ§Ъ§бЇ(ЮФПЦ) ЬтаЭЃК044
ШчЭМF1(ЃcЃЌ0)ЃЌF2(cЃЌ0)ЮЊЫЋЧњЯпEЕФСННЙЕуЃЌвдF1F2ЮЊжБОЖЕФдВOгыЫЋЧњЯпEНЛгкMЁЂNЁЂM1ЁЂN1ЃЌBЪЧдВOгыyжсЕФНЛЕуЃЌСЌНгMM1гыOBНЛгкHЃЌЧвHЪЧOBЕФжаЕуЃЌ

(1)ЕБcЃН1ЪБЃЌЧѓЫЋЧњЯпEЕФЗНГЬЃЛ
(2)ЪджЄЃКЖдШЮвтЕФе§ЪЕЪ§cЃЌЫЋЧњЯпEЕФРыаФТЪЮЊГЃЪ§ЃЛ
(3)СЌНгF1MгыЫЋЧњЯпEНЛгкЕуAЃЌЪЧЗёДцдкГЃЪ§![]() КуГЩСЂЃЌШєДцдкЪдЧѓГіІЫЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
КуГЩСЂЃЌШєДцдкЪдЧѓГіІЫЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃКНЫеЪЁГЃжнИпМЖжабЇ2007ЁЋ2008бЇФъЕкШ§ДЮНзЖЮНЬбЇжЪСПЕїбаИпШ§Ъ§бЇ(РэПЦ) ЬтаЭЃК044
ШчЭМF1(ЃcЃЌ0)ЃЌF2(cЃЌ0)ЮЊЫЋЧњЯпEЕФСННЙЕуЃЌвдF1F2ЮЊжБОЖЕФдВOгыЫЋЧњЯпEНЛгкMЁЂNЁЂM1ЁЂN1ЃЌBЪЧдВOгыyжсЕФНЛЕуЃЌСЌНгMM1гыOBНЛгкHЃЌЧвHЪЧOBЕФжаЕуЃЌ
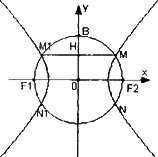
(1)ЕБcЃН1ЪБЃЌЧѓЫЋЧњЯпEЕФЗНГЬЃЛ
(2)ЪджЄЃКЖдШЮвтЕФе§ЪЕЪ§cЃЌЫЋЧњЯпEЕФРыаФТЪЮЊГЃЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com