
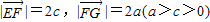 ,且
,且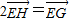 ,
,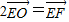 ,
,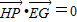 (G为动点).
(G为动点).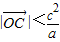 ;
;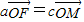 且点P的轨迹上存在点Q使得
且点P的轨迹上存在点Q使得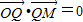 ,求点P的轨迹的离心率e的取值范围.
,求点P的轨迹的离心率e的取值范围.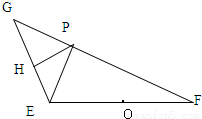
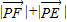 =
=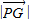 =2a,从而可得点P的轨迹是以E、F为焦点,长轴长为2a的椭圆,即可求轨迹方程;
=2a,从而可得点P的轨迹是以E、F为焦点,长轴长为2a的椭圆,即可求轨迹方程; ,即可求点P的轨迹的离心率e的取值范围.
,即可求点P的轨迹的离心率e的取值范围.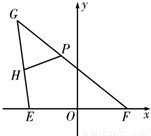 (1)解:如图,以EF所在的直线为x轴,EF的中垂线为y轴,建立平面直角坐标系.(1分)
(1)解:如图,以EF所在的直线为x轴,EF的中垂线为y轴,建立平面直角坐标系.(1分)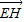 =
=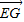 ,
,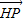 •
•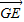 =0,
=0,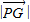 =
=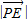 ,而
,而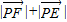 =
= =2a,
=2a,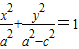 .(4分)
.(4分)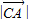 =
=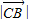 ,即(x1-x)2+
,即(x1-x)2+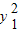 =(x2-x)2+
=(x2-x)2+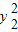 .①
.①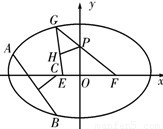
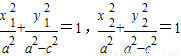 ,
,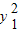 =
= ,(6分)
,(6分)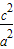 (
(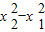 ),(8分)
),(8分)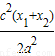 .(8分)
.(8分) ,即
,即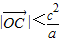 .(9分)
.(9分)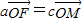 ,即点M为椭圆的右顶点,由
,即点M为椭圆的右顶点,由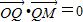 知直线OQ斜率必存在,
知直线OQ斜率必存在,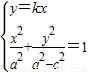 ,解得
,解得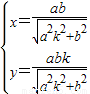 (其中b2=a2-c2) (11分)
(其中b2=a2-c2) (11分)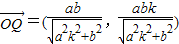
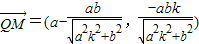
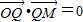 得
得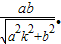
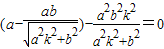
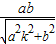 ,(12分)
,(12分)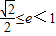
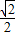 ,1)(14分)
,1)(14分)

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:高中数学 来源: 题型:
| 6 |

查看答案和解析>>
科目:高中数学 来源: 题型:
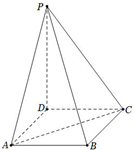 如图,已知:ABCD是矩形,AB=1,BC=2,PD⊥平面ABCD,且PD=3.
如图,已知:ABCD是矩形,AB=1,BC=2,PD⊥平面ABCD,且PD=3.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知圆G:x2+y2-2x-
如图,已知圆G:x2+y2-2x-| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 5 |
| 6 |
| FC |
| FD |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.
如图,已知长方体ABCD-A1B1C1D1中,AB=3,AD=AA1=2,点O是线段BC1的中点,点M是OD的中点,点E是线段AB上一点,AE>BE,且A1E⊥OE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com