【答案】
分析:(1)过C作CH⊥AB于H,根据AE⊥平面ABC,AE?平面AEDB,得到平面AEDB⊥平面ABC,结合线面面面垂直的性质证出CH⊥平面ABDE,从而得到CH就是四棱锥C-ABED的高,再用锥体的体积公式即可算出多面体ABCDE的体积;
(2)取BC中点M,连接AM、FM,由线面垂直的判定与性质,证出AM⊥平面BCD.再证出四边形AEFM是平行四边形,可得EF∥AM,由此即可得到EF⊥平面BCD;
(3)延长BA交DE延长线于N,连接BE,过A作AP∥BE,交DE于P,连接PC,可得当DF:FC=2:1时,AC∥平面EFB.再利用比例线段证出PC∥EF,结合线面平行的判定定理得到PC∥平面EFB,同理得到AP∥平面EFB,从而得到平面PAC∥平面EFB,可得AC∥平面EFB.
解答:解:(1)过C作CH⊥AB于H,
∵AE⊥平面ABC,AE?平面AEDB,∴平面AEDB⊥平面ABC,

∵平面AEDB∩平面ABC=AB,CH?平面ABC,CH⊥AB
∴CH⊥平面ABDE,可得CH就是四棱锥C-ABED的高
∵梯形ABDE的面积为S=

(AE+BD)•AB=3,CH=

AB=

∴多面体ABCDE的体积为:
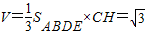
-------(6分)
(2)取BC中点M,连接AM、FM,
∵BD∥AE,AE⊥平面ABC,可得BD⊥平面ABC,∴BD⊥AM
∵正△ABC中,AM⊥CB,CB、BD是平面BCD内的相交直线,∴AM⊥平面BCD
∵AE∥BD且AE=

BD,在△BCD中,FM∥BD且FM=

BD
∴AE∥FM且AE=FM,由此可得四边形AEFM是平行四边形,可得EF∥AM
∴EF⊥平面BCD----------(10分)
(3)延长BA交DE延长线于N,连接BE,过A作AP∥BE,交DE于P,连接PC.
则当DF:FC=2:1时,AC∥平面EFB,证明如下
∵

,∴PC∥EF
∵PC?平面EFB,EF?平面EFB,∴PC∥平面EFB,同理可证AP∥平面EFB
∵PC、AP是平面PAC内的相交直线,∴平面PAC∥平面EFB
∵AC?平面PAC,∴AC∥平面EFB
即当

的值为2时,能使AC∥平面EFB---------------------(16分)
点评:本题给出特殊的四棱锥,求证线面垂直和线面平行并求了多面体的体积,着重考查了线面平面、面面平行的判定与性质,线面垂直、面面垂直的判定与性质和锥体体积公式等知识,属于中档题.

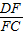 的值为多少时,能使AC∥平面EFB,并给出证明.
的值为多少时,能使AC∥平面EFB,并给出证明.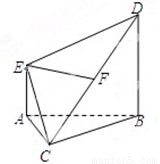

 (AE+BD)•AB=3,CH=
(AE+BD)•AB=3,CH= AB=
AB=
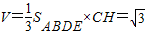 -------(6分)
-------(6分) BD,在△BCD中,FM∥BD且FM=
BD,在△BCD中,FM∥BD且FM= BD
BD ,∴PC∥EF
,∴PC∥EF 的值为2时,能使AC∥平面EFB---------------------(16分)
的值为2时,能使AC∥平面EFB---------------------(16分)

 如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1
如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1 如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC= (2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1=
(2012•青岛二模)如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,A1C=A1B,B1C1∥BC,B1C1= (2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1=
(2012•合肥一模)如图,在多面体ABC-A1B1C1中,AA1⊥平面ABC,AA1⊥平面ABC,AA1∥=BB1,AB=AC=AA1= (2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=
(2012•郑州二模)如图,在多面体ABC-A1B1C1中,四边形A1ABB1是正方形,AB=AC,BC=