
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
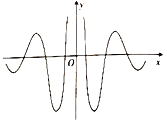
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
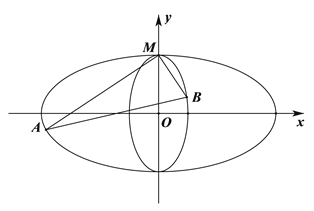
【题目】如图,焦点在![]() 轴上的椭圆
轴上的椭圆![]() 与焦点在
与焦点在![]() 轴上的椭圆
轴上的椭圆![]() 都过点
都过点![]() ,中心都在坐标原点,且椭圆
,中心都在坐标原点,且椭圆![]() 与
与![]() 的离心率均为
的离心率均为![]() .
.
(Ⅰ)求椭圆![]() 与椭圆
与椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)过点M的互相垂直的两直线分别与![]() ,
,![]() 交于点A,B(点A、B不同于点M),当
交于点A,B(点A、B不同于点M),当![]() 的面积取最大值时,求两直线MA,MB斜率的比值.
的面积取最大值时,求两直线MA,MB斜率的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的四个顶点,过E的左焦点F且不与坐标轴垂直的直线l与E交于A,B两点,线段AB的垂直平分线m与x轴,y轴分别交于M,N两点,交线段AB于点C.
的短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的四个顶点,过E的左焦点F且不与坐标轴垂直的直线l与E交于A,B两点,线段AB的垂直平分线m与x轴,y轴分别交于M,N两点,交线段AB于点C.
(1)求E的方程;
(2)设O为坐标原点,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,且
,且![]() ,当
,当![]() 时,求l的斜率的取值范围.
时,求l的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足,an+2=3an+1﹣2an,a1=1,a2=3,记bn![]() ,Sn为数列{bn}的前n项和.
,Sn为数列{bn}的前n项和.
(1)求证:{an+1﹣an}为等比数列,并求an;
(2)求证:Sn![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣tx+t.
(1)讨论f(x)的单调性;
(2)当t=2时,方程f(x)=m﹣ax恰有两个不相等的实数根x1,x2,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,P是椭圆的上顶点,过点P作斜率为
,P是椭圆的上顶点,过点P作斜率为![]() 的直线l交椭圆于另一点A,设点A关于原点的对称点为B
的直线l交椭圆于另一点A,设点A关于原点的对称点为B
(1)求![]() 面积的最大值;
面积的最大值;
(2)设线段PB的中垂线与y轴交于点N,若点N在椭圆内部,求斜率k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com