
【题目】已知圆![]() :
:![]() 关于直线
关于直线![]() :
:![]() 对称的圆为
对称的圆为![]() .
.
(Ⅰ)求圆![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 是坐标原点,是否存在这样的直线
是坐标原点,是否存在这样的直线![]() ,使得在平行四边形
,使得在平行四边形![]() (
(![]() 和
和![]() 为对角线)中
为对角线)中![]() ?若存在,求出所有满足条件的直线
?若存在,求出所有满足条件的直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(Ⅰ)![]() .(Ⅱ)存在直线
.(Ⅱ)存在直线![]() 和
和![]() .
.
【解析】
试题
本题考查圆方程的求法和直线与圆的位置关系。(Ⅰ)根据对称公式求得圆![]() 的圆心即可得到结果。(Ⅱ)由
的圆心即可得到结果。(Ⅱ)由![]() 得平行四边形
得平行四边形![]() 为矩形,故
为矩形,故![]() .然后分直线
.然后分直线![]() 的斜率存在与不存在两种情况,根据直线与圆的位置关系利用代数方法根据
的斜率存在与不存在两种情况,根据直线与圆的位置关系利用代数方法根据![]() 判断直线是否存在即可。
判断直线是否存在即可。
试题解析:
(Ⅰ)圆![]() 化为标准方程为
化为标准方程为![]() ,
,
设圆心![]() 关于直线
关于直线![]() :
:![]() 的对称点为
的对称点为![]() ,
,
由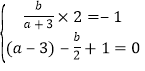 ,解得:
,解得:![]() ,
,
所以圆![]() 的圆心坐标为
的圆心坐标为![]() ,半径为3.
,半径为3.
故圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)由![]() ,得平行四边形
,得平行四边形![]() 为矩形,
为矩形,
所以![]() .
.
要使![]() ,必须满足
,必须满足![]() .
.
①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() ,
,
由![]() 解得
解得![]() 或
或 ![]()
直线![]() 与圆
与圆![]() 的两交点为
的两交点为![]() ,
,![]() .
.
因为![]() ,
,
所以![]() ,
,
即直线![]() :
:![]() 满足条件.
满足条件.
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
由![]() 消去y整理得
消去y整理得
![]() .
.
由于点![]() 在圆
在圆![]() 内部,所以
内部,所以![]() 恒成立,
恒成立,
设![]() ,
,![]()
则![]() ,
,![]() ,
,
所以![]()
![]() ,
,
整理得:![]()
解得![]() ,
,
所以直线![]() 的方程为
的方程为![]()
综上可得,存在直线![]() 和
和![]() ,使得在平行四边形
,使得在平行四边形![]() (
(![]() 和
和![]() 为对角线)中
为对角线)中![]() .
.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:
【题目】如图所示的等腰梯形ABCD中,![]() ,
,![]() ,E为CD中点.若沿AE将三角形DAE折起,并连接DB,DC,得到如图所示的几何体D-ABCE,在图中解答以下问题:
,E为CD中点.若沿AE将三角形DAE折起,并连接DB,DC,得到如图所示的几何体D-ABCE,在图中解答以下问题:

(1)设G为AD中点,求证:![]() 平面GBE;
平面GBE;
(2)若平面![]() 平面ABCE,且F为AB中点,求证:
平面ABCE,且F为AB中点,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体ABCD中,![]() 与
与![]() 都是边长为8的正三角形,点O是线段BC的中点.
都是边长为8的正三角形,点O是线段BC的中点.
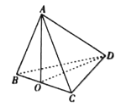
(1)证明:![]() .
.
(2)若![]() 为锐角,且四面体ABCD的体积为
为锐角,且四面体ABCD的体积为![]() 求侧面ACD的面积.
求侧面ACD的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,且
,且![]() ,
,![]()
(1)求证数列![]() 是等差数列,并求数列
是等差数列,并求数列![]() 的通项公式;
的通项公式;
(2)记![]() ,求
,求![]() ;
;
(3)是否存在实数k,使得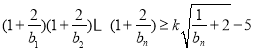 对任意
对任意![]() 都成立?若存在,求实数k的取值范围;若不存在,请说明理由.
都成立?若存在,求实数k的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生产基地有五台机器,现有五项工作待完成,每台机器完成每项工作后获得的效益值如表所示.若每台机器只完成一项工作,且完成五项工作后获得的效益值总和最大,则下列叙述错误的的是_____________.
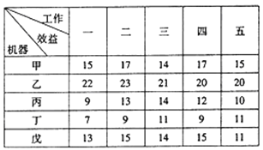
①甲只能承担第四项工作
②乙不能承担第二项工作
③丙可以不承担第三项工作
④丁可以承担第三项工作
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在含有![]() 个元素的集合
个元素的集合![]() 中,若这
中,若这![]() 个元素的一个排列(
个元素的一个排列(![]() ,
,![]() ,…,
,…,![]() )满足
)满足![]() ,则称这个排列为集合
,则称这个排列为集合![]() 的一个错位排列(例如:对于集合
的一个错位排列(例如:对于集合![]() ,排列
,排列![]() 是
是![]() 的一个错位排列;排列
的一个错位排列;排列![]() 不是
不是![]() 的一个错位排列).记集合
的一个错位排列).记集合![]() 的所有错位排列的个数为
的所有错位排列的个数为![]() .
.
(1)直接写出![]() ,
,![]() ,
,![]() ,
,![]() 的值;
的值;
(2)当![]() 时,试用
时,试用![]() ,
,![]() 表示
表示![]() ,并说明理由;
,并说明理由;
(3)试用数学归纳法证明:![]() 为奇数.
为奇数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,不过坐标原点
,不过坐标原点![]() 的直线
的直线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(Ⅰ)若![]() ,证明:直线
,证明:直线![]() 过定点;
过定点;
(Ⅱ)设过![]() 且与
且与![]() 相切的直线为
相切的直线为![]() ,过
,过![]() 且与
且与![]() 相切的直线为
相切的直线为![]() .当
.当![]() 与
与![]() 交于点
交于点![]() 时,求
时,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com