
坐标系与参数方程
已知圆锥曲线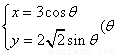 为参数)和定点
为参数)和定点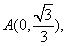 F1,F2是圆锥曲线的左右焦点。
F1,F2是圆锥曲线的左右焦点。
(1)求经过点F2且垂直于直线AF1的直线l的参数方程;
(2)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程。
(1) (2)
(2)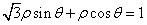
【解析】
试题分析:(1)利用三角函数中的平方关系消去参数θ,将圆锥曲线化为普通方程,从而求出其焦点坐标,再利用直线的斜率求得直线L的倾斜角,最后利用直线的参数方程形式,即可得到直线L的参数方程.
(2)设P(ρ,θ)是直线AF2上任一点,利用正弦定理列出关于ρ、θ的关系式,化简即得直线AF2的极坐标方程.
解:(1)圆锥曲线
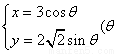 化为普通方程)
化为普通方程)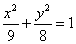
所以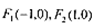 则直线
则直线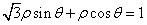 的斜率
的斜率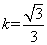
于是经过点 且垂直于直线
且垂直于直线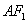 的直线l的斜率
的直线l的斜率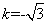
直线l的倾斜角为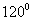
所以直线l参数方程 ,
,
(2)直线AF2的斜率k=- ,倾斜角是120°,设P(ρ,θ)是直线AF2上任一点即ρsin(120°-θ)=sin60°,化简得
,倾斜角是120°,设P(ρ,θ)是直线AF2上任一点即ρsin(120°-θ)=sin60°,化简得 ρcosθ+ρsinθ=
ρcosθ+ρsinθ= ,故可知
,故可知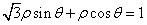
考点:曲线的极坐标方程、直线的参数方程
点评:本小题主要考查简单曲线的极坐标方程、直线的参数方程、椭圆的参数方程等基础知识,考查运算求解能力,考查数形结合思想.属于基础题


科目:高中数学 来源: 题型:
|
 |
| AP |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
|
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| π |
| 4 |
| y |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com