
【题目】对于在某个区间![]() 上有意义的函数
上有意义的函数![]() ,如果存在一次函数
,如果存在一次函数![]() 使得对于任意的
使得对于任意的![]() ,有
,有![]() 恒成立,则称函数
恒成立,则称函数![]() 是函数
是函数![]() 的一个弱渐近函数.
的一个弱渐近函数.
(1)若函数![]() 是函数
是函数![]() 在区间
在区间![]() 上的一个弱渐近函数,求实数
上的一个弱渐近函数,求实数![]() 的取值范围;
的取值范围;
(2)证明:函数![]() 是函数
是函数![]() 在区间
在区间![]() 上的弱渐近函数;
上的弱渐近函数;
(3)试问:函数![]() 与函数
与函数![]() (其中
(其中![]() 为自然对数的底数)在区间
为自然对数的底数)在区间![]() 上是否存在相同的弱渐近函数?如果存在,请求出对应的弱渐近函数应满足的条件;如不存在,请说明理由.
上是否存在相同的弱渐近函数?如果存在,请求出对应的弱渐近函数应满足的条件;如不存在,请说明理由.
【答案】(1)![]() ;(2)见解析;(3)存在,
;(2)见解析;(3)存在,![]() ,其中
,其中![]() .
.
【解析】
(1)由弱渐近函数的定义得出![]() ,由此可求出实数
,由此可求出实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,利用分子有理化结合放缩法证明出
时,利用分子有理化结合放缩法证明出![]() ,结合弱渐近函数的定义可证明结论成立;
,结合弱渐近函数的定义可证明结论成立;
(3)假设存在满足题意的弱渐近函数![]() ,根据弱渐近函数的定义得出
,根据弱渐近函数的定义得出![]() 和
和![]() ,可求得
,可求得![]() 以及实数
以及实数![]() 所满足的不等式组,解出即可得出满足题意的若渐近函数
所满足的不等式组,解出即可得出满足题意的若渐近函数![]() 的解析式.
的解析式.
(1)依题意,当![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 恒成立,故
恒成立,故![]() ,所以,实数
,所以,实数![]() 的取值范围是
的取值范围是![]() ;
;
(2)当![]() 时,
时,
![]()
![]() ,
,
![]() ,.
,.
故![]() ,得证;
,得证;
(3)假设存在满足题意的弱渐近函数![]() ,
,
![]() ,
,
若![]() ,由于当
,由于当![]() 时,
时,![]() ,故
,故![]() ,
,
但是,当![]() 时,
时,![]() ,故
,故![]() ,
,
不符合“![]() 恒成立”的要求,所以
恒成立”的要求,所以![]() ,
,
此时![]() ,则
,则![]() ,
,
解得:![]() ;
;
![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() ,
,
得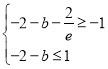 ,解得:
,解得:![]() .
.
综上所述,函数![]() 与函数
与函数![]() 在区间
在区间![]() 上存在相同的弱渐近函数,对应的弱渐近函数是
上存在相同的弱渐近函数,对应的弱渐近函数是![]() ,其中
,其中![]() .
.


科目:高中数学 来源: 题型:
【题目】已知集合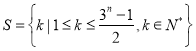 (
(![]() ,且
,且![]() ),若存在非空集合
),若存在非空集合![]() ,使得
,使得![]() ,且
,且![]() ,并任意
,并任意![]() ,都有
,都有![]() ,则称集合S具有性质P,
,则称集合S具有性质P,![]() 称为集合S的P子集.
称为集合S的P子集.
(1)当![]() 时,试说明集合S具有性质P,并写出相应的P子集
时,试说明集合S具有性质P,并写出相应的P子集![]() ;
;
(2)若集合S具有性质P,集合T是集合S的一个P子集,设![]() ,求证:任意
,求证:任意![]() ,
,![]() ,都有
,都有![]() ;
;
(3)求证:对任意正整数![]() ,集合S具有性质P.
,集合S具有性质P.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,焦点为
上,焦点为![]() ,圆O的直径为
,圆O的直径为![]() .
.

(1)求椭圆C及圆O的标准方程;
(2)设直线l与圆O相切于第一象限内的点P,且直线l与椭圆C交于![]() 两点.记
两点.记![]() 的面积为
的面积为![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国已进入新时代中国特色社会主义时期,人民生活水平不断提高.某市随机统计了城区若干户市民十月人均生活支出比九月人均生活支出增加量(记为P元)的情况,并根据统计数据制成如图频率分布直方图.
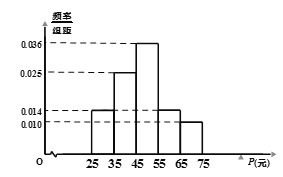
(1)根据频率分布直方图估算P的平均值![]() ;
;
(2)若该市城区有4户市民十月人均生活支出比九月人均生活支出分别增加了42元,50元,52元,60元,从这4户中随机抽取2户,求这2户P值的和超过100元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1所示,在直角梯形DCEF中,![]() ,
,![]() ,
,![]() ,
,![]() ,将四边形ABEF沿AB边折成图2.
,将四边形ABEF沿AB边折成图2.
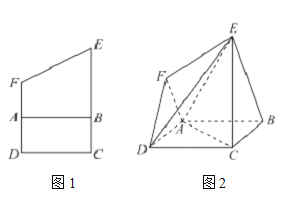
(1)求证:![]() 平面DEF;
平面DEF;
(2)若![]() ,求平面DEF与平面EAC所成锐二面角的余弦值.
,求平面DEF与平面EAC所成锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com