Question

（08年黄冈中学二模）如图，直三棱柱A₁B₁C₁―ABC中，C₁C=CB=CA=2，AC⊥CB. D、E分别为棱C₁C、B₁C₁的中点.

    （Ⅰ）求与平面A₁C₁CA所成角的大小；

    （Ⅱ）求二面角B―A₁D―A的大小；

    （Ⅲ）试在线段AC上确定一点F，使得EF⊥平面A₁BD.

 

Answer 1

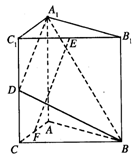
解析：（Ⅰ）连接A₁C.∵A₁B₁C₁－ABC为直三棱柱，∴CC₁⊥底面ABC，∴CC₁⊥BC.

       ∵AC⊥CB，∴BC⊥平面A₁C₁CA.

       ∴为与平面A₁C₁CA所成角，.

∴与平面A₁C₁CA所成角为.

（Ⅱ）分别延长AC，A₁D交于G. 过C作CM⊥A₁G 于M，连结BM，

       ∵BC⊥平面ACC­₁A₁，∴CM为BM在平面A₁C₁CA内的射影，

       ∴BM⊥A₁G，∴∠CMB为二面角B―A₁D―A的平面角，

       平面A₁C₁CA中，C₁C=CA=2，D为C₁C的中点，

       ∴CG=2，DC=1 在直角三角形CDG中，，.

       即二面角B―A₁D―A的大小为.

（Ⅲ）取线段AC的中点F，则EF⊥平面A₁BD.

证明如下：

∵A₁B₁C₁―ABC为直三棱柱，∴B₁C₁//BC，

∵由（Ⅰ）BC⊥平面A₁C₁CA，∴B₁C₁⊥平面A₁C₁CA，

∵EF在平面A₁C₁CA内的射影为C₁F，当F为AC的中点时，

C₁F⊥A₁D，∴EF⊥A₁D.

同理可证EF⊥BD，∴EF⊥平面A₁BD.

解法二：

（Ⅰ）同解法一

（Ⅱ）∵A₁B₁C₁―ABC为直三棱柱，C₁C=CB=CA=2，

AC⊥CB，D、E分别为C₁C、B₁C₁的中点.

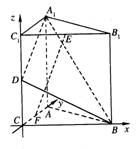
建立如图所示的坐标系得：

C（0，0，0），B（2，0，0），A（0，2，0），

C₁（0，0，2）， B₁（2，0，2）， A­₁（0，2，2），

D（0，0，1）， E（1，0，2）.

，设平面A₁BD的法向量为，

  .

平面ACC₁A₁­的法向量为=（1，0，0），.

即二面角B―A₁D―A的大小为.

（Ⅲ）F为AC上的点，故可设其坐标为（0，，0），∴.

由（Ⅱ）知是平面A₁BD的一个法向量，

欲使EF⊥平面A₁BD，当且仅当// 

∴，∴当F为AC的中点时，EF⊥平面A₁BD.