Question

设a、b、c分别是△ABC中∠A、∠B、∠C的对边,其外接圆半径为1,且(sinB+sinC+sinA)(sinB+sinC-sinA)=3sinBsinC,b、c是方程x²-3x+4cosA=0的两根(b＞c).

(1)求角A的度数及a、b、c的值;

(2)判定△ABC的形状,并求其内切圆的半径.

Answer 1

解:(1)由韦达定理b+c=3,b·c=4cosA,由正弦定理b=2RsinB=2sinB,c=2sinC.

∴2(sinB+sinC)=3,sinB·sinC=cosA.

∵（sinB+sinC+sinA）(sinB+sinC-sinA)=3sinBsinC,

    利用平方差公式展开为（sinB+sinC）²-sin²A=3sinBsinC,

    把sinB＋sinC＝,sinB·sinC=cosA代入上式可得-sin²A=3cosA.

    整理得4cos²A-12cosA+5=0,

    即(2cosA-5)(2cosA-1)=0,

∴cosA=,cosA=(舍去).

∴∠A=60°.∴

∵b＞c,∴b=2,c=1.

    由余弦定理a²=b²+c²-2bccosA=2²+1²-2×2×1×=3,∴a=.

(2)∵b²=a²+c²(由勾股定理).

∴△ABC是直角三角形.

    如图所示,设内切圆半径是r,则∠OAB=30°,

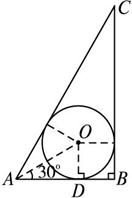
    在△OAD中,AD=rcot30°=r,∴r+r=1.∴内切圆半径r=.