
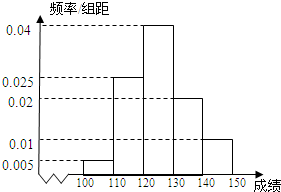
 长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图.
长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图. ,
, =105×0.05+115×0.25+125×0.4+135×0.2+145×0.1=125.5(分).
=105×0.05+115×0.25+125×0.4+135×0.2+145×0.1=125.5(分). ,则
,则 =105×0.05+115×0.25+125×0.4+135×0.2+145×0.1,运算求得结果.
=105×0.05+115×0.25+125×0.4+135×0.2+145×0.1,运算求得结果.

科目:高中数学 来源: 题型:
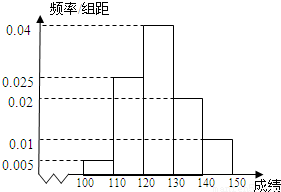
 长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图.
长春市某中学高三(1)班40名学生在一次数学测验中,成绩全部介于100分与150分之间,将测验成绩按如下方式分成五组:第一组[100,110);第二组[110,120),…,第五组[140,150].右图是按上述分组方法得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源:2010年吉林省长春市农安实验中学高考数学冲刺试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com