
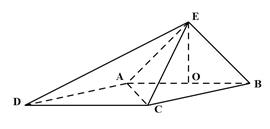
已知四棱锥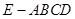 的底面为菱形,且
的底面为菱形,且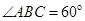 ,
,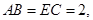
 ,
,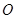 为
为 的中点.
的中点.
(Ⅰ)求证: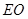
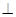 平面
平面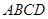 ;
;
(Ⅱ)求点 到面
到面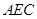 的距离.
的距离.
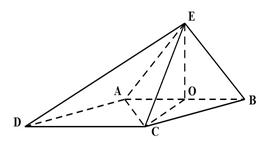
(I)证明:连接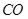
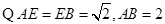
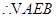 为等腰直角三角形
为等腰直角三角形

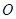 为
为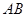 的中点
的中点
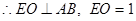 ……………………2分
……………………2分
得出 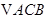 是等边三角形
是等边三角形
由勾股定理得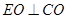 ,
,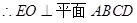
(II)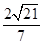 。
。
【解析】
试题分析:(I)证明:连接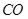
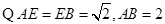
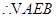 为等腰直角三角形
为等腰直角三角形

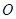 为
为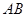 的中点
的中点
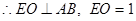 ……………………2分
……………………2分
又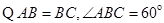
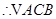 是等边三角形
是等边三角形
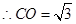 ,………………………………4分
,………………………………4分
又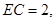
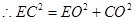 ,即
,即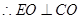
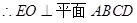 ……………………6分
……………………6分
(II)设点 到面
到面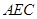 的距离为
的距离为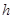
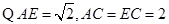

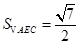 …………8分
…………8分

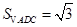 ,
,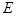 到面
到面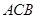 的距离
的距离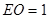
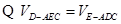

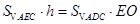 ………………………………10分
………………………………10分
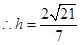
 点
点 到面
到面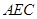 的距离为
的距离为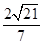 ……………………12分
……………………12分
考点:本题主要考查立体几何中的垂直关系,体积及距离的计算。
点评:中档题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,利用向量则能简化证明过程。本题计算距离时运用了“等体积法”,简化了解答过程。


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:2013年普通高等学校招生全国统一考试安徽卷文数 题型:044
如图,四棱锥P-ABCD的底面ABCD是边长为2的菱形,∠BAD=60°.已知PB=PD=2,PA=![]() .
.
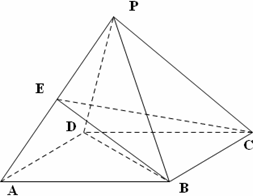
(Ⅰ)证明:PC⊥BD.
(Ⅱ)若E为PA的中点,求三菱锥P-BCE的体积.
查看答案和解析>>
科目:高中数学 来源:2013年全国普通高等学校招生统一考试文科数学(安徽卷解析版) 题型:解答题
如图,四棱锥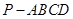 的底面
的底面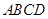 是边长为2的菱形,
是边长为2的菱形,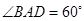 .已知
.已知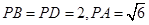 .
.
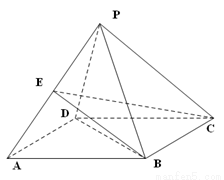
(Ⅰ)证明: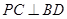
(Ⅱ)若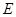 为
为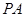 的中点,求三菱锥
的中点,求三菱锥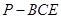 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com