
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 根据题意,建立平面直角坐标系,用坐标表示向量,利用∠AOC=30°,即可求得结论
解答 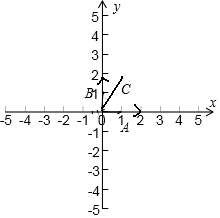 解:∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,∴$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,
解:∵$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,∴$\overrightarrow{OA}$⊥$\overrightarrow{OB}$,
建立如图所示的平面直角坐标系:
则$\overrightarrow{OA}$=(2,0),$\overrightarrow{OB}$=(0,$\sqrt{3}$),∵$\overrightarrow{OC}$=m$\overrightarrow{OA}$+n$\overrightarrow{OB}$,
∴$\overrightarrow{OC}$=(2m,$\sqrt{3}$n),
∵∠AOC=60°,∴tan60°=$\frac{\sqrt{3}n}{2m}$=$\sqrt{3}$
∴$\frac{m}{n}$=$\frac{1}{2}$;
故选:A.
点评 本题考查向量知识的运用,考查向量的坐标运算,考查学生的计算能力,关键是正确建系,利用坐标法解答;属于中档题.


科目:高中数学 来源: 题型:解答题
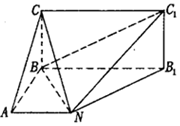 如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.
如图,已知矩形BB1C1C所在平面与底面ABB1N垂直,在直角梯形ABB1N中,AN∥BB1,AB⊥AN,CB=BA=AN=$\frac{1}{2}$BB1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+2i | B. | 1-2i | C. | 2-i | D. | 2+i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
| 化学分数z | 67 | 72 | 76 | 80 | 84 | 87 | 90 | 92 |
| 优秀 | 不优秀 | 合计 | |
| 数学 | |||
| 物理 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
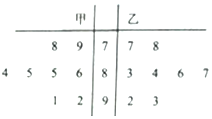 甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )
甲、乙两名同学八次数学测试成绩如茎叶图所示,则甲同学成绩的众数与乙同学成绩的中位数依次为( )| A. | 85,86 | B. | 85,85 | C. | 86,85 | D. | 86,86 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知函数f(x)=x3+ax2+bx,(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为3,则a的值为$-\sqrt{6}$.
已知函数f(x)=x3+ax2+bx,(a,b∈R)的图象如图所示,它与直线y=0在原点处相切,此切线与函数图象所围区域(图中阴影部分)的面积为3,则a的值为$-\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {2} | C. | {3,4} | D. | {1,2,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com