
如图,已知正三棱柱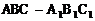 的各条棱长都为a,P为
的各条棱长都为a,P为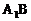 上的点。(1)试确定
上的点。(1)试确定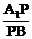 的值,使得PC⊥AB;
的值,使得PC⊥AB;
(2)若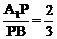 ,求二面角P—AC—B的大小;
,求二面角P—AC—B的大小;
(3)在(2)的条件下,求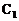 到平面PAC的距离。
到平面PAC的距离。
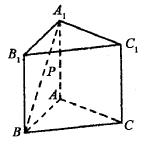
解:以A为原点,AB为x轴,过A点与AB垂直的直线为y轴,AA1为z轴,建立空间直角坐标系A—xyz,如图所示,则B(a,0,0),A1(0,0,a),C( ,
, ,0),设P(x,0,z)
,0),设P(x,0,z)

(1)由 ,得
,得
即 ,∴P为A1B的中点
,∴P为A1B的中点
即 时,PC⊥AB
.
……………………3分
时,PC⊥AB
.
……………………3分
(2)当 时,由
时,由 ,得(x,0,z-a)
,得(x,0,z-a)
即
设平面PAC的一个法向量
则 ,即
,即
即
取 ,则
,则
∴
又平面ABC的一个法向量为
∴
∴二面角P—AC—B的大小为180°-120°=60°………………7分
(3)设C1到平面PAC的距离为d
则
即C1到平面PAC的距离为 .
……………………10分
.
……………………10分
注:以上答案只能是个参考。


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com