解:(Ⅰ)∵A
1、A
2是双曲线的左、右顶点,∴A
1(-2,0)A
2(2,0)
∵MN是双曲线
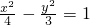
的弦,且MN与x轴垂直,∴设M(x
0,y
0),则N(x
0,-y
0)
则直线MA
1和NA
2的方程分别为y=

(x+2),y=
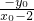
(x-2)
联立两方程,解x
0,y
0,得
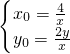
,∵M(x
0,y
0)在双曲线上,代入双曲线方程,得

,即直线MA
1和NA
2的交点的轨迹C的方程为

(Ⅱ)联立
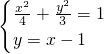
得7x
2-8x-8=0
由韦达定理得
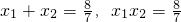
A,B,P三点在

上,
知3x
12+4y
12=12,3x
22+4y
22=12,
∵
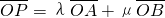
,∴P点坐标为(λ
2x
12+2λμx
1x
2+μ
2x
22,λ
2y
12+2λμy
1y
2+μ
2y
22)
∴3(λ
2x
12+2λμx
1x
2+μ
2x
22)+4(λ
2y
12+2λμy
1y
2+μ
2y
22)=12
又
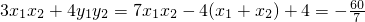
∴

∴
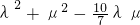
为定值,且定制为1.
分析:(Ⅰ)利用交轨法来求直线MA
1和NA
2的交点的轨迹方程,先根据已知条件求出A
1、A
2点的坐标,设M(x
0,y
0),则N(x
0,-y
0),求出直线MA
1和NA
2的方程,联立方程,方程组的解为直线MA
1和NA
2交点的坐标,再把M点坐标(x
0,y
0)用x,y表示,代入双曲线方程,化简即得轨迹C的方程.
(Ⅱ)联立直线y=x-1与轨迹C方程,解出A,B点横坐标之和与之积,因为P,A,B三点都在椭圆上,所以都满足椭圆方成,再根据
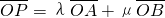
,得到三点坐标满足的关系式,把P点坐标用A,B坐标表示,代入椭圆方程,根据前面求出的x
1+x
2,x
1x
2的值,化简,即可得到
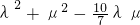
的值,为定植.
点评:本题主要考查了交轨法求轨迹方程,以及直线与圆锥曲线相交问题,注意韦达定理的应用.

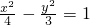 的弦,且MN与x轴垂直,A1、A2是双曲线的左、右顶点.
的弦,且MN与x轴垂直,A1、A2是双曲线的左、右顶点.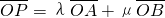 (O为坐标原点,λ,μ∈R)
(O为坐标原点,λ,μ∈R)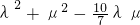 为定值,并求出这个定值.
为定值,并求出这个定值.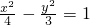 的弦,且MN与x轴垂直,∴设M(x0,y0),则N(x0,-y0)
的弦,且MN与x轴垂直,∴设M(x0,y0),则N(x0,-y0) (x+2),y=
(x+2),y=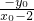 (x-2)
(x-2)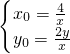 ,∵M(x0,y0)在双曲线上,代入双曲线方程,得
,∵M(x0,y0)在双曲线上,代入双曲线方程,得 ,即直线MA1和NA2的交点的轨迹C的方程为
,即直线MA1和NA2的交点的轨迹C的方程为
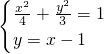 得7x2-8x-8=0
得7x2-8x-8=0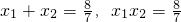
 上,
上,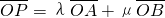 ,∴P点坐标为(λ2x12+2λμx1x2+μ2x22,λ2y12+2λμy1y2+μ2y22)
,∴P点坐标为(λ2x12+2λμx1x2+μ2x22,λ2y12+2λμy1y2+μ2y22)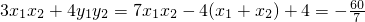

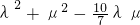 为定值,且定制为1.
为定值,且定制为1.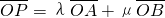 ,得到三点坐标满足的关系式,把P点坐标用A,B坐标表示,代入椭圆方程,根据前面求出的x1+x2,x1x2的值,化简,即可得到
,得到三点坐标满足的关系式,把P点坐标用A,B坐标表示,代入椭圆方程,根据前面求出的x1+x2,x1x2的值,化简,即可得到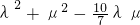 的值,为定植.
的值,为定植.

 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 的弦,且MN与x轴垂直,A1、A2是双曲线的左、右顶点.
的弦,且MN与x轴垂直,A1、A2是双曲线的左、右顶点. (O为坐标原点,λ,μ∈R)
(O为坐标原点,λ,μ∈R) 为定值,并求出这个定值.
为定值,并求出这个定值.