
 (θ为参数)上求一点,使它到直线C2:
(θ为参数)上求一点,使它到直线C2: (t为参数)的距离最小,并求出该点的坐标和最小距离.
(t为参数)的距离最小,并求出该点的坐标和最小距离. (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为:
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为: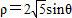 .
. ,求|PA|+|PB|.
,求|PA|+|PB|.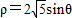 ,得
,得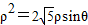 ,进而可化为普通方程.
,进而可化为普通方程.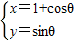 (θ为参数)化为普通方程(x-1)2+y2=1.
(θ为参数)化为普通方程(x-1)2+y2=1.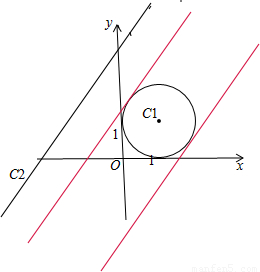
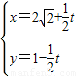 (t为参数)消去参数t化为普通方程x+y=
(t为参数)消去参数t化为普通方程x+y= .
. 消去y得到(x-1)2+(x-t)2=1,即2x2-2(1+t)x+t2=0,
消去y得到(x-1)2+(x-t)2=1,即2x2-2(1+t)x+t2=0,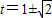 ,
,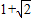 时,切点M到直线C2:x+y=
时,切点M到直线C2:x+y=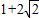 的距离最小,此时,由方程
的距离最小,此时,由方程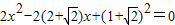 解得
解得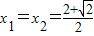 ,得y=
,得y=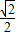 ,
,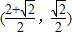 .
.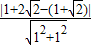 =1.
=1.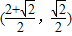 ,1.
,1.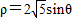 ,∴
,∴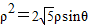 ,∴
,∴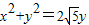 ,即
,即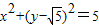 .
.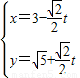 (t为参数),消去参数t化为普通方程x+y=3+
(t为参数),消去参数t化为普通方程x+y=3+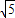 .
.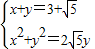 解得
解得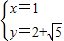 或
或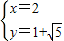 ,不妨设A(1,
,不妨设A(1,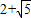 ),B(2,1
),B(2,1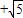 ),
),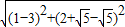 +
+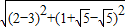 =
=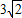 .
.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
| 生产能力分组 | [100,110] | [110,120] | [120,130] | [130,140] | [140,150] |
| 人数 | 4 | 8 | x | 5 | 3 |
| 生产能力分组 | [110,120] | [120,130] | [130,140] | [140,150] |
| 人数 | 6 | y | 36 | 18 |
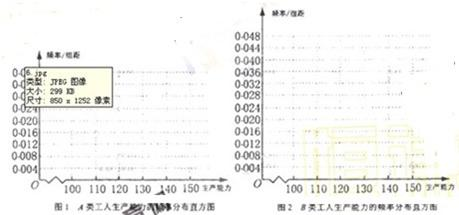
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| n |
 |
| i=1 |
| 机器号 | 初始时 | 第一单位时间 | 第二单位时间 | 第三单位时间 | |||
| 被读机号 | 结 果 | 被读机号 | 结 果 | 被读机号 | 结 果 | ||
| 1 | v1 | 2 | v1+v2 | ||||
| 2 | v2 | 1 | v2+v1 | ||||
| 机器号 | 初始时 | 第一单位时间 | 第二单位时间 | 第三单位时间 | |||
| 被读机号 | 结 果 | 被读机号 | 结 果 | 被读机号 | 结 果 | ||
| 1 | v1 | ||||||
| 2 | v2 | ||||||
| 3 | v3 | ||||||
| 4 | v4 | ||||||
| n |
 |
| i=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.
(文科做)已知点A1(2,0),A2(1,t),A3(0,b),A4(-1,t),A5(-2,0),其中t>0,b为正常数.查看答案和解析>>
科目:高中数学 来源: 题型:
| 第一项技术指标 | 第二项技术指标 | |
| 甲 | 0.8 | 0.85 |
| 乙 | 0.75 | 0.8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com