

(1)证明AB1∥平面DBC1;
(2)假设AB1⊥BC1,求以BC1为棱,DBC1与CBC1为面的二面角α的度数.
(1)证明:连结B1C、DC1、DB、BC1,并设B1C∩BC1=E,连结DE.
∵ABC—A1B1C1为正三棱柱,
则B1BCC1为矩形,∴E为B1C的中点.
又D为AC的中点,
∴DE![]()
![]() AB1,DE
AB1,DE![]() 平面DBC1.
平面DBC1.
∴AB1∥平面DBC1.
(2)解析:∵平面ABC⊥平面BCC1B1,作AG⊥BC于G,则AG⊥平面 BCC1B1,DF⊥BC于F,则DF⊥平面BCC1B1,且DF=![]() AG.
AG.
∵AB1⊥BC1,AB1∥DE,
∴DE⊥BC1,DF⊥平面BCC1.
∴EF⊥BC1.
∴∠DEF为二面角DBC1C的平面角.
在△ABC中,设边长为a.
EG⊥BF,EF2=FG·FB,EF=![]() a,DF=
a,DF=![]() AG=
AG=![]() a,
a,
∴∠DEF=45°.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:
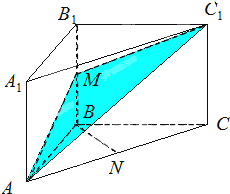 如图,ABC-A1B1C1是直三棱柱(侧棱与底面垂直的三棱柱叫直三棱柱),M是BB1的中点,N是AC的中点;
如图,ABC-A1B1C1是直三棱柱(侧棱与底面垂直的三棱柱叫直三棱柱),M是BB1的中点,N是AC的中点;查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•芜湖三模)如图,正三棱柱ABC-A1B1C1中,E是AC中点.
(2012•芜湖三模)如图,正三棱柱ABC-A1B1C1中,E是AC中点.| 2 |
| A1A |
| AB |
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:022
一个直三棱柱ABC![]() A1B1C1的容器中盛有水,AA1=4.如图,若以面AA1B1B为底面水平放置时,液面恰好过AC、BC、A1C1、B1C1的中点.则以面ABC为底面水平放置时,液面高等于________.
A1B1C1的容器中盛有水,AA1=4.如图,若以面AA1B1B为底面水平放置时,液面恰好过AC、BC、A1C1、B1C1的中点.则以面ABC为底面水平放置时,液面高等于________.

查看答案和解析>>
科目:高中数学 来源:2012-2013学年云南省昭通市水富县高一(上)期末数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com