解:(1)f′(x)=ae
x+2x-a.设g(x)=ae
x+2x-a,
则g′(x)=ae
x+2>0恒成立,故g(x)在R上是增函数,
即f′(x)是增函数,
又f′(0)=a-a=0,
∴当x<0;由f′(x)<0,当x>0;由f′(x)>0,
∴f(x)的单调增区间(0,+∞),单调减区间(-∞,0);
(2)设F(x)=f(x)-f(-x)=a(e
x-e
-x-2x),则F′(x)=a(e
x+e
-x-2),
∵a>0,e
x+e
-x≥2,∴F′(x)≥0,当且仅当x=0时取等号,
所以F(x)在R是增函数,且F(0)=0,
∴F(x)>0?x∈(0,+∞),
∴不等式f(x)>f(-x)的解集(0,+∞);
(3)由题意知,f′(x
0)=k=

=
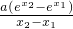
+(x
2+x
1)-a,
f′(

)=ae
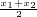
+(x
2+x
1)-a,
∴f′(x
0)-f′(

)=
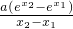
-ae
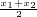
,
设t=

,则
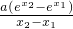
÷(ae
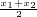
)=
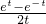
,
当t>0时,由(2)知,e
t-e
-t-2t>0,∴
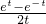
>1,
当t<0时,由(2)知,e
t-e
-t-2t<0,∴
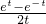
>1,
即
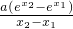
>ae
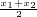
,
∴f′(x
0)-f′(

)>0,
又由(1)知,f′(x)是增函数,
∴x
0>

.
分析:(1)先求函数的导函数f′(x),并将其因式分解,便于解不等式,再由f′(x)>0,得函数的单调增区间,由f′(x)<0,得函数的单调减区间;
(2)先设F(x)=f(x)-f(-x)=a(e
x-e
-x-2x),将解不等式的问题转化为研究函数的最值问题.利用导数工具得出F(x)在R是增函数,从而求出不等式f(x)>f(-x)的解集;
(3)根据直线的斜率公式得f′(x
0)=k,再计算出f′(

),作差f′(x
0)-f′(

)=
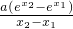
-ae
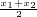
,设t=

,再作商
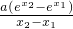
÷(ae
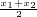
)=
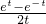
,最后利用(1)(2)中的结论即可证出结论.
点评:本题考查了利用导数求函数的单调区间的方法,已知函数的单调区间求参数范围的方法,体现了导数在函数单调性中的重要应用;不等式恒成立问题的解法,转化化归的思想方法

 .
. =
=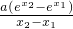 +(x2+x1)-a,
+(x2+x1)-a, )=ae
)=ae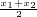 +(x2+x1)-a,
+(x2+x1)-a, )=
)=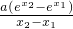 -ae
-ae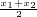 ,
, ,则
,则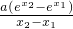 ÷(ae
÷(ae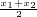 )=
)=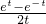 ,
,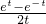 >1,
>1,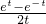 >1,
>1,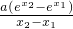 >ae
>ae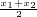 ,
, )>0,
)>0, .
. ),作差f′(x0)-f′(
),作差f′(x0)-f′( )=
)=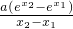 -ae
-ae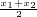 ,设t=
,设t= ,再作商
,再作商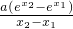 ÷(ae
÷(ae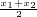 )=
)=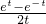 ,最后利用(1)(2)中的结论即可证出结论.
,最后利用(1)(2)中的结论即可证出结论.
